Wonk post: Circular security

Apologies in advance for a super-wonky post, but I’m in kind of a wonky mood this week. It happens that I’m putting together a talk on the subject of circular security, and I figured this blog might be a good place to get my thoughts together.

If you’ve never heard of circular security, don’t feel bad — you’re in good company. In a nutshell, circular security describes the way that an encryption scheme behaves when you ask it to encrypt its own key. In theory, that behavior can be pretty unpredictable.

The key word in the previous sentence is ‘theory’. Circular security is a very interesting research area, but if your primary reason for reading this blog is to learn about practical things, this post may not be for you. (Though please come back next week, when I hope to be writing about electronic cash!)

Assuming you’re still reading, the first order of business is to talk about what circular security (or insecurity) is in the first place. To do that, we need to define what it means for an encryption scheme to be ‘secure’. And that means a discussion of semantic security.

Semantic Security

Semantic security is one of the earliest and most important security definitions in our field. It’s generally considered to be the minimum bar for any modern ‘secure’ encryption scheme. In English, the informal definition of semantic security is something like this:

An attacker who sees the encryption of a message — drawn from a known, or even chosen message space — gains approximately the same amount of information as they would have obtained if they didn’t see the encryption in the first place. (The one exception being the length of the message.)

This is a nice, intuitive definition since it captures what we really want from encryption.

You see, in an ideal world, we wouldn’t need encryption at all. We would send all of our data via some sort of magical, buried cable that our adversary couldn’t tap. Unfortunately, in the real world we don’t have magical cables: we send our data via the public WiFi at our neighborhood Starbucks.

Semantic security tells us not to worry. As long as we encrypt with a semantically-secure scheme, the adversary who intercepts our encrypted data won’t learn much more than the guy who didn’t intercept it at all — at worst, he’ll learn only the amount of data we sent. Voila, security achieved.

(Now, just for completeness: semantic security is not the strongest definition we use for security, since it does not envision active attacks, where the adversary can obtain the decryption of chosen ciphertexts. But that’s a point for another time.)

Unfortunately, before we can do anything with semantic security, we need to turn the English-language intuition above into something formal and mathematical. This is surprisingly complicated, since it requires us to formalize the notion of ‘an attacker gains approximately the same amount of information‘. In the early definitions this was done by making grand statements about predicate functions. This approach is faithful and accurate. It’s also kind of hard to do anything with.

Fortunately there’s a much simpler, yet equivalent way to define semantic security. This definition is called ‘indistinguishability under chosen plaintext attack‘, or IND-CPA for short. IND-CPA is described by the following game which is ‘played’ between an adversary and some honest party that we’ll call the challenger:

The challenger generates a public/private keypair, and gives the public key to the adversary.
The adversary eventually picks two equal-length messages (M0, M1) from the set of allowed plaintexts, and sends them to the challenger.
The challenger flips a coin, then returns the encryption of one of the messages under the public key.
The attacker tries to guess which message was encrypted. He ‘wins’ if he guesses correctly.

(This game can also be applied to symmetric encryption. Since there’s no public key in a symmetric scheme, the challenger makes up the lost functionality by providing an encryption oracle: i.e., it encrypts messages for the adversary as she asks for them.)

A quick glance at the game should convince you that even a moron adversary can win this game. In fact, if the adversary simply guesses randomly he’ll be right exactly half the time. Hence the real question is: how much better can he do?

And that leads us to our (basically) formal definition:

A scheme is IND-CPA secure if no adversary can win the above game with probability (significantly) greater than 1/2.

The term ‘significantly’ in this case hides a lot of detail — typically it means that ‘non-negligibly‘. In many schemes we also require the adversary to run in limited time (i.e., be a probabilistic polynomial-time Turing machine). But details, details…

Encrypting your own key

One of the weirder aspects of the IND-CPA definition above is that it doesn’t handle a very basic (and surprisingly common!) use case: namely, cases where you encrypt your own secret key.

Believe it or not, this actually happens. If you use a disk encryption system like Bitlocker, you maybe already be encrypting your own keys, without even noticing it. Moreover, newer schemes like Gentry’s Fully Homomorphic Encryption depend fundamentally on this kind of “circular” encryption.

It seems surprising that IND-CPA can give us such a strong notion of security — where the attacker learns nothing about a plaintext — and yet can’t handle this very simple case. After all, isn’t your secret key just another message? What makes it special?

The technical answer to this question hangs on the fact that the IND-CPA game above only works with messages chosen by the adversary. Specifically, the adversary is asked to attack the encryption of either M0 or M1, which he chooses in step (2). Since presumably — if the scheme is secure — the adversary doesn’t know the scheme’s secret key, he won’t be able to submit (M0,M1) such that either message contains the scheme’s secret key. (Unless he makes a lucky guess, but this should happen with at most negligible probability.)

What this means is that an encryption scheme could do something terribly insecure when asked to encrypt its own secret key. For example, it could burp out the secret key without encrypting it at all! And yet it would still satisfy the IND-CPA definition. Yikes! And once you raise the possibility that such a scheme could exist, cryptographers will immediately wants to actually build it.

(This may seem a little perverse: after all, aren’t there enough broken schemes in the world without deliberately building more? But when you think about it, this kind of ‘counterexample’ is extremely valuable to us. If we know that such oddball, insecure schemes can exist, that motivates to watch out for them in the real constructions that we use. And it tells us a little about the strength of our definitions.)

It turns out that there’s a ‘folklore’ approach that turns any IND-CPA secure public-key encryption scheme into one that’s still IND-CPA secure, but is also totally insecure if it ever should encrypt its own secret key.

The basic approach is to modify the original scheme by changing the encryption algorithm as follows:

On input a public key and a message to be encrypted, it tests to see if the message is equal to the scheme’s secret key.*
If not, it encrypts the message using the original scheme’s encryption algorithm (which, as we noted previously, is IND-CPA secure).
If the message is equal to the secret key, it just outputs the secret key in cleartext.

It’s pretty easy to see that this scheme is as secure as the original scheme for messages that aren’t the secret key. It’s also easy to see that it’s totally insecure when you do encrypt the actual secret key. (Though I’ve glossed over a small technical challenge in step 2, see footnote*).

Circles and cycles

Just as cryptographers were congratulating each other for answering the previous question — showing that there are schemes that fail catastrophically when they encrypt their own secret key — some smartass decided to up the stakes.

The question (s)he asked was: what if two people encrypt each other’s secret keys?

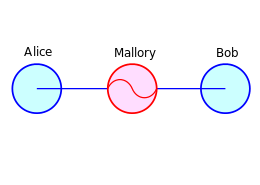
Let’s be clear what I’m saying here. Imagine that Alice decides to entrust Bob with her secret key, so she wraps it up under his public key (say, sending him a PGP encrypted email). And imagine that Bob decides to do exactly the same with his key, encrypting it under Alice’s public key. We now have the following ‘key cycle’:

CA = Encrypt(pkA, skB), CB = Encrypt(pkB, skA)

To be clear, IND-CPA by itself tells us that it’s perfectly secure for Alice to encrypt her own key under Bob’s key (or vice versa). There’s no problem there. However, the minute Bob also encrypts Alice’s secret key, a cycle is formed — and semantic security doesn’t tell us anything about whether this is secure.

So this is worrisome in theory, but are there actual schemes where such cycles can cause problem?

Up until 2010, the answer was: no. It turns out to be much harder to find a counterexample for this case, since the approach described in the previous section doesn’t work. You can’t just hack a little bit of code into the encryption algorithm; the ciphertexts are encrypted independently. At the time they’re encrypted, the ciphertexts are perfectly secure. They only become insecure when they come into close proximity with one another.

(If a weird analogy helps, think of those encrypted keys like two hunks of Plutonium, each inside of its own briefcase. As long as they’re apart, everything’s fine. But get them close enough to one another, they interact with one another and basically ruin your whole day.)

It gets worse

A breakthrough occurred at Eurocrypt 2010, where Acar, Belenkiy, Bellare and Cash showed that indeed, there is a scheme that’s perfectly IND-CPA secure in normal usage, but fails when Alice and Bob encrypt their keys in a cycle like the one described above.

The Acar et al. scheme is based on certain type of elliptic-curve setting known as bilinear SXDH, and what they show is that when Alice and Bob create a key cycle like the one above, an adversary can recognize it as such.

To be clear, what this means is that the ciphertexts (Encrypt(pkA, skB), Encrypt(pkB, skA)) jointly leak a little bit of information — simply the fact that they encrypt each other’s secret keys! This may not seem like much, but it’s far more than they should ever reveal.

The Acar et al. result is interesting to me, because along with my colleague Susan Hohenberger, I was thinking about the same problem around the same time. We independently came up with a similar finding just a few months after Acar et al. submitted theirs — crappy luck, but it happens. On the bright side, we discovered something slightly worse.

Specifically, we were able to construct a scheme that’s totally secure in normal usage, but becomes catastrophically insecure the minute Alice and Bob encrypt each others’ secret keys. This means in practice that if two parties innocently encrypt a key cycle, then both of their secret keys become public. This means every message that either party has ever encrypted (or will encrypt) becomes readable. Not good!**

The worst part is that both the Acar et al. scheme and our scheme are (almost) normal-looking constructions. They could be real schemes that someone came up with and deployed in the real world! And if they did, and if someone encrypted their secret keys in a cycle, things would be very bad for everyone.

So what do we do about this?

The solution to this problem is to develop schemes that can handle (by design) the case where someone encrypts a secret key, or a function of a secret key. This concept is known as Key-Dependent Message (KDM) security, and it’s been the subject of some research.

Unfortunately, building provably KDM-secure schemes is not an easy task, at least, not without resorting to artificial constructs like random oracles. While this may change in the future, for the moment we have a ways to go before we can build truly efficient schemes that don’t (potentially) have problems like the above.

And this is what makes cryptography so interesting. No matter what we say about our schemes being ‘provably secure’, the truth is: there’s always something we haven’t thought of. Just when you thought you’d finally solved all the major security problems (ha!), another one will always pop up to surprise you.

Notes:

* The obvious objection is that a public key encryption algorithm takes in only a public key and a message. It doesn’t take in the scheme’s secret key. So: how can it check whether the given message is the encryption of the secret key? There’s a general solution to this, but I’ll leave it as an exercise for the reader.

** David Cash, Susan Hohenberger and I have summarized these results, along with several related to symmetric encryption, and will be presenting them at PKC 2012. If you’re interested, a full version of our paper should appear here shortly.

So long False Start, we hardly knew ye

Last week brought the sad news that Google is removing support for TLS False Start from the next version of Chrome. This follows on Google’s decision to withdraw TLS Snap Start, and caps off the long line of failures that started with the demise of Google Wave. Industry analysts are already debating the implications for Larry Page’s leadership and Google’s ‘Social’ strategy.

(I am, of course, being facetious.)

More seriously, it’s sad to see False Start go, since the engineering that led to False Start is one of the most innovative things happening in Internet security today. It’s also something that only Google can really do, since they make a browser and run a very popular service. The combination means they can try out new ideas on a broad scale without waiting for IETF approval and buy-in. Nor are they shy about doing this: when the Google team spots a problem, they tackle it head-on, in what I call the ‘nuke it from orbit’ approach. It’s kind of refreshing.

Of course, the flipside of experimentation is failure, and Google has seen its share of failed experiments. The last was Snap Start, which basically tackled the same problem as False Start, but in a different way. And now False Start is going the way of the coelacanth: it’ll still exist, but you’ll have a hard time finding it.

The response from the security community has been a lot of meaningful chin-tapping and moustache-stroking, but not (surprisingly) a lot of strong opinions. This is because — as we all recently discovered — none of us had really spent much time thinking about False Start before Google killed it.* And so now we’re all doing it retroactively.

What the heck is (was) False Start anyway?

Secure web (TLS) is dirt slow. At least, that’s the refrain you’ll hear from web companies that don’t deploy it. There are many objections but they usually boil down to two points: (1) TLS requires extra computing hardware on the server side, and (2) it adds latency to the user experience.

Why latency? Well, to answer that you only need to look at the TLS handshake. The handshake establishes a communication key between the server and client. It only needs to happen once per browsing session. Unfortunately it happens at the worst possible time: the first time you visit a new site. You never get a second chance to make a first impression.

Why is the standard handshake so slow? Short answer: key establishment requires two round trips — four ‘flights’ — before the client can send any actual data (say, an HTTP GET request). If you’re communicating via undersea cable, or if you’re using a mobile phone with a huge ping time (my AT&T phone just registered 250ms!) this is going to add up.

Standard TLS handshake (source). Application data exchange only occurs at step (9) in the diagram. Note that step (5) is optional, and steps (4),(7) can be conducted in the same message ‘flight’.

This is the problem that False Start tried to address. The designers — Langley, Modadugu and Moeller — approached this in the simplest possible way: they simply started sending data earlier.

You see, the bulk of the key exchange work in TLS really occurs in the first three messages, “client hello”, “server hello”, and “client key exchange”. By the time the client is ready to send this last message, it already knows the encryption key. Hence it can start transmitting encrypted data right then, cutting a full roundtrip off the handshake. The rest of the handshake is just ‘mop-up’: mostly dedicated to ensuring that nobody tampered with the handshake messages in-flight.

If your reaction to the previous sentence was: ‘isn’t it kind of important to know that nobody tampered with the handshake messages?‘, you’ve twigged to the primary security objection to False Start. But we’ll come back to that in a moment.

False Start sounds awesome: why did Google yank it?

The problem with False Start is that there are many servers (most, actually) that don’t support it. The good news is that many of them will tolerate FS. That is, if the Client starts sending data early, they’ll hold onto the data until they’ve finished their side of the handshake.

But not every server is so flexible. A small percentage of the servers on the Internet — mostly SSL terminators, according to Langley — really couldn’t handle False Start. They basically threw up all over it.

Google knew about this before deploying FS in Chrome, and had taken what I will loosely refer to as the ‘nuke it from orbit squared‘ approach. They scanned the Internet to compile a blacklist list of IPs that didn’t handle False Start, and they shipped it with Chrome. In principle this should have done the job.

Unfortunately, it didn’t. It seems that the non-FS-compatible servers were non-compliant in a weird non-deterministic way. A bunch looked good when Google scanned them, but really weren’t. These slipped past Google’s scan, and ultimately Google gave up on dealing with them. False Start was withdrawn.

**Ok, it has issues. But is it secure?**

From my point of view this is the much more interesting question. A bunch of smart folks (and also: me) wasted last Friday afternoon discussing this on Twitter. The general consensus is that we don’t really know.

The crux of the discussion is the Server “finished” message (#8 in the diagram above). This message is not in TLS just for show: it contains a hash over all of the handshake messages received by the server. This allows the client to verify that no ‘man in the middle’ is tampering with handshake messages, and in normal TLS it’s supposed to verify this before it sends any sensitive data.

This kind of tampering isn’t theoretical. In the bad old days of SSL2, it was possible to quietly downgrade the ciphersuite negotiation so that the Browser & Server would use an ‘export-weakened’ 40-bit cipher even when both wanted to use 128-bit keys. Integrity checks (mostly) eliminate this kind of threat.

The FS designers were wise to this threat, so they include some mitigations to deal with it. From the spec:

Clients and servers MUST NOT use the False Start protocol modification in a handshake unless the cipher suite uses a symmetric cipher that is considered cryptographically strong … While an attacker can change handshake messages to force a downgrade to a less secure symmetric cipher than otherwise would have been chosen, this rule ensures that in such a downgrade attack no application data will be sent under an insecure symmetric cipher.

While this seems to deal with the obvious threats (‘let’s not use encryption at all!’), it’s not clear that FS handles every possible MITM threat that could come up. For example, there were a number of mitigations proposed to deal with the BEAST attack — from basic things like ‘don’t use TLS 1.0’ to ‘activate the empty-fragment’ protection. There’s some reason to be fearful that these protections could be overwhelmed or disabled by an attacker who can tamper with handshake messages.

Note that this does not mean that False Start was actually vulnerable to any of the above. The last thing I want to do is claim a specific vulnerability in FS. Or rather, if I had a specific, concrete vulnerability, I’d be blogging about it.

Rather, the concern here is that TLS has taken a long time to get to the point it is now — and we’re still finding bugs (like BEAST). When you rip out parts of the anti-tamper machinery, you’re basically creating a whole new world of opportunities for clever (or even not-so-clever) attacks on the protocol. And that’s what I worry about.

Hands off my NSS

There’s one last brief point I’d like to mention about False Start and Snap Start, and that has to do with the implementation. If you’ve ever spent time with the NSS or OpenSSL code, you know that these are some of the finest examples of security coding in the world.

Haha, I kid. They’re terrifying.

Every time Google adds another extension (Snap Start, False Start, etc.), NSS gets patched. This additional patch code is small, and it’s written by great coders — but even so, this patching adds new cases and complexity to an already very messy library. It would be relatively easy for a bug to slip into one of these patches, or even the intersection of two patches. And this could affect more than just Google users.

In summary

It may seem a little odd to spend a whole blog post on a protocol that’s already been withdrawn, but really: it’s worth it. Examining protocols like False Start is the only way we learn; and making TLS faster is definitely something we want to learn about. Second, it’s not like False Start is the last we’ll hear from the Google TLS crew. It’ll certainly help if we’re up-to-speed when they release “False Start II: False Start with a Vengeance”.

Finally, False Start isn’t really dead — not yet, anyway. It lives on in Chrome for conducting Next Protocol Negotiation (NPN) transactions, used to negotiate SPDY.

On a final note, let me just say that I’m mostly enthusiastic about the work that Google is doing (modulo a few reservations noted above). I hope to see it continue, though I would like to see it get a little bit more outside scrutiny. After all, even though Google’s primarily acting as its own test case, many people use Chrome and Google! If they get something wrong, it won’t just be Google doing the suffering.

Notes:

* With some notable exceptions: see this great presentation by Nate Lawson.

It’s the end of the world as we know it (and I feel fine)

Unitards: another consequence
of quantum computing.

Back in December I asked readers for some topics they were particularly keen to read about on this blog. One of the best (and sadly, most challenging) suggestions was to say something about post-quantum cryptography. Roughly speaking, this term describes the future of cryptography after quantum computers arrive and screw things up for everyone.

Now, just for the record, quantum computing is not a bad thing; in fact, it’s one of the most exciting discoveries of our time. At minimum QCs will help us efficiently solve challenging problems that take forever on today’s computers. It’s entirely possible, though not guaranteed, that they’ll totally revolutionalize the way we compute (see this breathless article). Whichever it is, quantum computers will be a general good.

But not necessarily for cryptographers.

This is because cryptographers don’t always want faster algorithms for solving hard problems. It isn’t that we thrive on people’s frustration; it’s that many of our best cryptosystems simply depend on the hardness of problems like integer factorization. By making these problems easy, QCs throw a huge wrench into the works. And this isn’t a hypothetical concern: thanks to Shor’s algorithm, many of our most beloved cryptosystems are already living on borrowed time.

But all is not lost. We have two very important things working in our favor. The first is time. For all the excitement around quantum computing, nobody’s managed to actually build a useful one. And (no matter what D-Wave says) it doesn’t look like they will anytime soon.

The second is that quantum computers are not magic. QCs are very good at quickly solving certain problems, but their usefulness is more limited than most people realize. Moreover, we only know of a handful of useful quantum algorithms today. This could change: think how many classical algorithms were discovered after classical computers were built. But it gives us hope.

In the rest of this post I’m going to try to give a flavor of the problem, and point out some of the bright spots — areas where we feel pretty good. I want to be clear that this isn’t my research area, and many of the best ideas in this post come from the excellent book Post-Quantum Cryptography, edited by Bernstein, Buchmann and Dahmen. (A dead-tree copy of the book will run you $90, but you can check out Dan Berstein’s fantastic intro right here.)

Quantum vs. Classical

Quantum computers are only human. (Well, technically,
they’re complicated machines full of super-cooled liquid
nitrogen and helium.)

There are many ways to build a classical computer. Whether you use transistors, gears, or photons, one thing binds all of these designs together: at any given moment, a classical computer should be in exactly one state.

To bring this back to cryptography, let’s say you’re trying to brute-force your way through the keyspace of a cryptosystem. In a classical computer this means trying one key at a time, for as many keys as it takes to get a useful result. Parallelization can speed this up, but ultimately just moves the problem sideways — trading resources for time.

Quantum computers use an entirely different model of computing. The fundamental component of a quantum computer is a quantum bit (‘qubit’), a value that can be in two states (1 and 0) at the same time. By entangling n qubits, it’s possible to construct a computer that exists in a ‘superposition’ of 2^n states simultaneously. And this is when things get interesting.

And complicated. Entrangling qubits is one thing (and not necessarily an easy thing). The real trick is finding a way to do computation with a computer that’s in more than one state, and — even more importantly — to pull a single ‘right’ answer back into our classical world once the computation is done.

These words obscure a lot of detail; an entire field’s worth of detail. What matters for our purposes is that in some cases it seems like quantum algorithms can harness this power to accomplish things much faster than classical algorithms. When this happens, it makes certain problems much easier (i.e., less time-consuming) to solve. But not every problem.

Quantum computers are not magic!

The important thing to know is that quantum computers can’t do everything. They can’t see the future. They can’t even (we believe) solve NP-complete problems in polynomial time. In fact, the general belief among researchers is that the class BQP — roughly, things that quantum computers can do efficiently — does not include all of NP (though in fairness, nobody knows for sure).

Proposed hierarchy of complexity classes
with a guess for where BQP may fit. (Wikipedia)

More importantly, anything that a quantum computer can do can also be done by a classical computer, though possibly with an exponential slowdown. This means that QCs aren’t going to do anything against information-theoretically secure cryptosystems, like the One Time Pad. Those schemes don’t care how powerful the attacker’s computer is.

Given these facts, you might not all that impressed with quantum computers right now. You’d be wrong.

An algorithm for a computer that doesn’t exist

The reason we’re so freaked out about quantum computing

is because of the harmless-looking gentleman above. Dr. Peter Shor claims responsibility for one of the most amazing, yet ostensibly useless, theoretical accomplishments in the history of computing: he developed a polynomial-time algorithm for factoring large integers. The only problem is that nobody has a computer that can run it.

I can only imagine how he explains this to his neighbors.

Shor’s algorithm actually has two components: (1) a classical portion that converts the factoring problem into an order-finding problem. And (2) a quantum portion that solves the latter in polynomial time (with some reasonable error probability). Shor’s algorithm can also be used to solve the Discrete Logarithm Problem (DLP) in fields and (with tweaks) elliptic curve groups.

The problem? Almost every practical public-key cryptosystem in use today depends on the hardness of the above problems. That includes RSA and Diffie-Hellman (both used in TLS), Elgamal (used in PGP), DSA and ECDSA (used to sign X.509 certificates, among other things), and even the Rabin cryptosystem (used primarily by Bram Cohen).

These are important algorithms, used today not just to protect short-term data, but also to encrypt data that may be still be important several decades from now. If anyone manages to build a reasonable quantum computer in that time, some people are going to be pretty unhappy.

I should quickly mention that Shor’s algorithm is not the only quantum algorithm that cryptographers care about — it just happens to be the most interesting one. There’s also Grover’s algorithm, which can be used to improve brute-force attacks on symmetric encryption schemes like AES. But the speedup from Grover’s algorithm is ‘only’ quadratic (it essentially halves the key length), not exponential like Shor’s algorithm. We can live with quadratic.

So what can we do about it?

With all the background out of the way, we can finally get to the point of this post. What can cryptographers do to deal with the looming potential of quantum computers? And when should we start doing it? There are a few answers to this question.

Solution #1: Business as usual

This is probably my favorite solution. Don’t do anything. Quantum computing is a long way off, and it may never happen at all. Let’s just keep doing what we’re doing, until we’re old enough that someone gives us a pension and we can dump the problem in someone else’s lap. Besides, isn’t there an asteroid heading towards the Earth?

No, this isn’t really a solution at all, but it seems to be the default mentality right now. It probably isn’t hurting us — for the moment.

Solution #2: Don’t overreact

While Shor’s algorithm is a pretty serious threat to RSA, (EC)DSA and most of the public-key algorithms we use in practice, these aren’t the only algorithms that we use. And the good news is that quantum computers probably won’t have the same effect on those.

AES, for example, would be affected by Grover’s algorithm, but only (in the absolute absurdly worst case), by reducing the effective key size by half. So a 256-bit key would still provide at least the same security margin as today’s 128-bit keys. We can probably live with that — and if not, we can always get bigger keys.

The only hole in this argument is that we have absolutely no idea what specific attacks people will develop against ciphers like AES in the future . Even now — using only classical algorithms — researchers have managed to shave a couple of bits off of the AES security margin. Quantum computers may substantially expand our toolbox.

Solution #3: Lattices, lattices, lattices!

(source/cc)

If you haven’t been to a crypto conference lately, you haven’t been exposed to the new hotness in our field: lattice-based cryptography. Lattices are a mathematical structure that happens to turn up a lot in nature: for example, in the ordering of atoms in a crystal.

In a more abstract setting, lattice ‘problems’ — can be used to build a wide variety of cryptosystems. The best known examples include the NTRU scheme (used for encryption and signature) and Craig Gentry’s fully-homomorphic encryption scheme. But there are plenty more.

Lattices get a lot of attention these days, in part because you can do neat things with them (fully-homomorphic encryption is a great example). But a more general argument for lattice-based crypto is its resistance to quantum attacks. In contrast to factoring and DLP, there are no quantum algorithms known to run (substantially) faster than classical algorithms against the lattice problems we use to construct modern cryptosystems.

As with all of these claims, the keyword is ‘known’. Will we someday find such algorithms? Who knows. But deploying schemes that aren’t quantum-broken (yet) certainly feels a lot better than deploying schemes that are.

Solution #4: Fight fire with fire

QKD rig. (image source)

The last, and possibly most desperate solution of all, is to dispense with computational problems altogether, and simply use the strength of quantum mechanics against itself.

This type of cryptography is known Quantum Key Distribution. QKD uses quantum-mechanical effects, rather than hard computational problems, to protect messages transmitted over a long distance.

The basic idea is quite simple: anyone who measures the quantum state of a particle must by definition change it (physics students: you’re welcome to correct me here!). The exception is entangled particles, which will both measure identically, even if the measurement is conducted at distant points. QKD rigs entangle particles, then transmit one set to a remote party via a long fiber-optic cable. If an attacker taps the cable and measures the particle, his tampering will be detected. If not, both parties can derive a random one-time pad, which they can then use to communicate. Quantum computers can’t do anything about this.

Unfortunately the more ‘perfect’ something sounds, the less you should trust it, especially if it’s a research system. This is what QKD researchers discovered last summer, when a team showed how to override the photon detectors in a QKD system with adversarially-generated signals of their own. The result: they were able to completely intercept the key without detection. This can all be fixed, but it goes to show that this is a harder problem than it looks.

More to the point, QKD requires a massive change in the way we distribute data. Today we send our ciphertexts through packet-switched networks, but QKD systems require dedicated fiber-optic connections between each participant. Thus, QKD isn’t likely to give us a good replacement for TLS anytime soon.

In summary

This has been yet another long post. Before I wrap up I just want to preemptively apologize to all of the physicists and quantum complexity theorists whose work I’ve mangled along the way.

No matter how terribly I’ve done this, the basic story is sound: quantum computers are at least theoretically possible, they’re quite likely to be practical, and they really will change a lot of things when they arrive. Mostly for the better. But not for the cryptosystems we use today.

If we don’t find a way to do something about this, the next few decades are going to be a very interesting time for crypto. For this reason alone, I’m hoping that asteroid isn’t coming; I’d really like to see how it all turns out.

iCloud: Who holds the key?

Ars Technica brings us today’s shocking privacy news: ‘Apple holds the master decryption key when it comes to iCloud security, privacy‘. Oh my.

The story is definitely worth a read, though it may leave you shaking your head a bit. Ars’s quoted security experts make some good points, but they do it in a strange way — and they propose some awfully questionable fixes.

But maybe I’m too picky. To be honest, I didn’t realize that there was even a question about who controlled the encryption key to iCloud storage. Of course Apple does — for obvious technical reasons that I’ll explain below. You don’t need to parse Apple’s Terms of Service to figure this out, which is the odd path that Ars’s experts have chosen:

In particular, Zdziarski cited particular clauses of iCloud Terms and Conditions that state that Apple can “pre-screen, move, refuse, modify and/or remove Content at any time” if the content is deemed “objectionable” or otherwise in violation of the terms of service. Furthermore, Apple can “access, use, preserve and/or disclose your Account information and Content to law enforcement authorities” whenever required or permitted by law.

Well, fine, but so what — Apple’s lawyers would put stuff like this into their ToS even if they couldn’t access your encrypted content. This is what lawyers do. These phrases don’t prove that Apple can access your encrypted files (although, I remind you, they absolutely can), any more than Apple’s patent application for a 3D LIDAR camera ‘proves’ that you’re going to get one in your iPhone 5.

Without quite realizing what I was doing, I managed to get myself into a long Twitter-argument about all this with the Founder & Editor-in-Chief of Ars, a gentleman named Ken Fisher. I really didn’t mean to criticize the article that much, since it basically arrives at the right conclusions — albeit with a lot of nonsense along the way.

Since there seems to be some interest in this, I suppose it’s worth a few words. This may very well be the least ‘technical’ post I’ve ever written on this blog, so apologies if I’m saying stuff that seems a little obvious. Let’s do it anyway.

The mud puddle test

You don’t have to dig through Apple’s ToS to determine how they store their encryption keys. There’s a much simpler approach that I call the ‘mud puddle test’:

First, drop your device(s) in a mud puddle.
Next, slip in said puddle and crack yourself on the head. When you regain consciousness you’ll be perfectly fine, but won’t for the life of you be able to recall your device passwords or keys.
Now try to get your cloud data back.

Did you succeed? If so, you’re screwed. Or to be a bit less dramatic, I should say: your cloud provider has access to your ‘encrypted’ data, as does the government if they want it, as does any rogue employee who knows their way around your provider’s internal policy checks.

And it goes without saying: so does every random attacker who can guess your recovery information or compromise your provider’s servers.

Now I realize that the mud puddle test doesn’t sound simple, and of course I don’t recommend that anyone literally do this — head injuries are no fun at all. It’s just a thought experiment, or in the extreme case, something you can ‘simulate’ if you’re willing to tell your provider few white lies.

But you don’t need to simulate it in Apple’s case, because it turns out that iCloud is explicitly designed to survive the mud puddle test. We know this thanks to two iCloud features. These are (1) the ability to ‘restore’ your iCloud backups to a brand new device, using only your iCloud password, and (2) the ‘iForgot’ service, which lets you recover your iCloud password by answering a few personal questions.

Since you can lose your device, the key isn’t hiding there. And since you can forget your password, it isn’t based on that. Ergo, your iCloud data is not encrypted end-to-end, not even using your password as a key (or if it is, then Apple has your password on file, and can recover it from your security questions.) (Update: see Jonathan Zdziarski’s comments at the end of this post.)

You wanna make something of it?

No! It’s perfectly reasonable for a consumer cloud storage provider to design a system that emphasizes recoverability over security. Apple’s customers are far more likely to lose their password/iPhone than they are to be the subject of a National Security Letter or data breach (hopefully, anyway).

Moreover, I doubt your median iPhone user even realizes what they have in the cloud. The iOS ‘Backup’ service doesn’t advertise what it ships to Apple (though there’s every reason to believe that backed up data includes stuff like email, passwords, personal notes, and those naked photos you took.) But if people don’t think about what they have to lose, they don’t ask to secure it. And if they don’t ask, they’re not going to receive.

My only issue is that we have to have this discussion in the first place. That is, I wish that companies like Apple could just come right out and warn their users: ‘We have access to all your data, we do bulk-encrypt it, but it’s still available to us and to law enforcement whenever necessary’. Instead we have to reverse-engineer it by inference, or by parsing through Apple’s ToS. That shouldn’t be necessary.

But can’t we fix this with Public-Key Encryption/Quantum Cryptography/ESP/Magical Unicorns?

No, you really can’t. And this is where the Ars Technica experts go a little off the rails. Their proposed solution is to use public-key encryption to make things better. Now this is actually a great solution, and I have no objections to it. It just won’t make things better.

To be fair, let’s hear it in their own words:

First, cloud services should use asymmetric public key encryption. “With asymmetric encryption, the privacy and identity of each individual user” is better protected, Gulri said, because it uses one “public” key to encrypt data before being sent to the server, and uses another, “private” key to decrypt data pulled from the server. Assuming no one but the end user has access to that private key, then no one but the user—not Apple, not Google, not the government, and not hackers—could decrypt and see the data.

I’ve added the boldface because it’s kind of an important assumption.

To make a long story short, there are two types of encryption scheme. Symmetric encryption algorithms have a single secret key that is used for both encryption and decryption. The key can be generated randomly, or it can be derived from a password. What matters is that if you’re sending data to someone else, then both you and the receiver need to share the same key.

Asymmetric, or public-key encryption has two keys, one ‘public key’ for encryption, and one secret key for decryption. This makes it much easier to send encrypted data to another person, since you only need their public key, and that isn’t sensitive at all.

But here’s the thing: the difference between these approaches is only related to how you encrypt the data. If you plan to decrypt the data — that is, if you ever plan to use it — you still need a secret key. And that secret key is secret, even if you’re using a public-key encryption scheme.

Which brings us to the real problem with all encrypted storage schemes: someone needs to hold the secret decryption key. Apple has made the decision that consumers are not in the best position to do this. If they were willing to allow consumers to hold their decryption keys, it wouldn’t really matter whether they were using symmetric or public-key encryption.

So what is the alternative?

Well, for a consumer-focused system, maybe there really isn’t one. Ultimately people back up their data because they’re afraid of losing their devices, which cuts against the idea of storing encryption keys inside of devices.

You could take the PGP approach and back up your decryption keys to some other location (your PC, for example, or a USB stick). But this hasn’t proven extremely popular with the general public, because it’s awkward — and sometimes insecure.

Alternatively, you could use a password to derive the encryption/decryption keys. This approach works fine if your users pick decent passwords (although they mostly won’t), and if they promise not to forget them. But of course, the convenience of Apple’s “iForgot” service indicates that Apple isn’t banking on users remembering their passwords. So that’s probably out too.

In the long run, the answer for non-technical users is probably just to hope that Apple takes good care of your data, and to hope you’re never implicated in a crime. Otherwise you’re mostly out of luck. For tech-savvy users, don’t use iCloud and do try to find a better service that’s willing to take its chances on you as the manager of your own keys.

In summary

I haven’t said anything in this post that you couldn’t find in Chapter 1 of an ‘Intro to Computer Security’ textbook, or a high-level article on Wikipedia. But these are important issues, and there seems to be confusion about them.

The problem is that the general tech-using public seems to think that cryptography is a magical elixir that can fix all problems. Companies — sometimes quite innocently — market ‘encryption’ to convince people that they’re secure, when in fact they’re really not. Sooner or later people will figure this out and things will change, or they won’t and things won’t. Either way it’ll be an interesting ride.

Update 4/4: Jonathan Zdziarski ‏tweets to say my ‘mud puddle’ theory is busted: since the iForgot service requires you to provide your birthdate and answer a ‘security question’, he points out that this data could be used as an alternative password, which could encrypt your iCloud password/keys — protecting them even from Apple itself.

The problem with his theory is that security answers don’t really make very good keys, since (for most users) they’re not that unpredictable. Apple could brute-force their way through every likely “hometown” or “favorite sport” in a few seconds. Zdziarski suggests that Apple might employ a deliberately slow key derivation function to make these attacks less feasible, and I suppose I agree with him in theory. But only in theory. Neither Zdziarski or I actually believe that Apple does any of this.

Poker is hard, especially for cryptographers

I have this friend who’s an obsessive poker fan, to the point where it’s actually a little scary. The worst part is that as a computer scientist, he approaches the game with a numeracy that would make an Apollo 11 technician blush. He refuses to touch a hand until he’s computed the precise odds, which wouldn’t be so bad if he didn’t tell me about it — all while gibbering mysterious 19th-century words like ‘flop’ and ‘river’ and ‘hole card’.

When this happens I try to smile and nod like I have some idea what he’s talking about. But trust me, I don’t. My card-playing experience runs to a few tense games of ‘Go Fish!’ and a drunken weekend in Vegas playing Blackjack.

Still, there’s one aspect of card playing that I am fascinated by: mental poker. This is a blanket term for a protocol that allows mutually-distrustful people to deal and play cards without a dealer, or, indeed, any trusted party at all.

Like all crypto/privacy protocols, mental poker interests me because it’s so counterintuitive. You get a bunch of people together, none of whom trust each other — some of whom may be actively trying to cheat the others — and at the end of the day everyone gets a fair deal, or at worst, enough warning to get out clean.

I also love the concept because it’s so obviously disruptive. In case you hadn’t heard, US law enforcement doesn’t have warm, cuddly feelings towards online poker. This past spring, the FBI took down three of the biggest sites, and there’s no reason to think they’re done. I may not be a poker player myself, but decentralized mental poker appeals to me, mostly because it would be a lot harder to shut down — especially if it was tied to a peer-to-peer currency such as Bitcoin. (On the other hand, you’d be playing for Bitcoin. So there’s that.)

In the rest of this post I’m going to talk a little bit about where mental poker came from and how it works. I don’t plan to give too many equations, but it will get a little (or a lot) wonky, and will certainly depart a bit from the pro-implementer, pro-engineering spirit of this blog. (If you want to pass, I certainly won’t hold it against you.)

Secret history

Like every other problem in our field, ‘Mental poker’ was first proposed by Shamir, Rivest and Adleman (note to self: invent new research field, get dibs on all the interesting problems.) Their motivation was — well, let’s just let them tell it:

Once there were two “mental chess” experts who had become tired of their favorite pastime. Let’s play “mental poker” for some variety suggested one. “Sure” said the other. “Just let me deal!”

In that first paper, Shamir et al. managed the fascinating trick of both proving that mental poker is impossible, and then giving a protocol to do it securely. (Don’t get discouraged by this — it happens.)

While the Shamir et al. paper may have been the first to address mental poker, it definitely wasn’t the last. Indeed, it’s an open secret that most of the ‘fundamental’ advances in cryptography — semantically-secure encryption, zero-knowledge proofs, etc. — were actually just happy accidents: things that dropped out while MIT cryptographers were fiendishly seeking better ways to play Five Card Stud with their colleagues at Weizmann.

Whether you believe this or not, the fact is that mental poker is really challenging, and did motivate a lot of new work. To explain this, let’s go over the basics of the problem.

Face up or Face Down?

For a mental poker scheme to be useful, it has to achieve three basic goals:

The shuffle must be random.
The deck must be correct — no trick aces!
Some cards must be dealt face down.

Let’s focus on the last point for a moment. If you’ve ever toyed with the idea of writing a card game, you probably know how to represent face-up cards: just let each be an integer from 0 through 51. Obviously we’ll need a table to map those values into something that humans can work with, but fundamentally this is no sweat.

Face-down cards, on the other hand, are more complicated. We need a publicly-visible data structure that can do what a physical card does: it must commit the holder to a particular face value. At the same time, it must hide that value from everyone else.

The simple and elegant solution (in case you didn’t see it coming) is to encrypt the face-down cards using a semantically-secure encryption scheme such as Elgamal.

(A quick note: ‘semantic security’ is a fundamental security definition that’s considered the minimum bar for every modern encryption scheme. In english, it means that you can’t learn any useful information from a ciphertext. It goes without saying that the definition was proposed in a paper about mental poker.)

While encryption solves some of our problems, it doesn’t quite solve them all. In fact, it gives us a big new one. If we’re going to encrypt the cards, who the heck is going to hold the decryption key?

And this is where modern public-key cryptography really shines. A basic trick is that every player can generate a ‘share’ of the decryption key such that the sum of all those shares is the decryption key for the entire scheme (they can also use these shares to generate the public key). This allows the players to cooperatively decrypt any ciphertext, such that no individual player ever gets the entire decryption key.

And now we have almost enough to describe a ‘simple’ mental poker protocol.

Generate the deck. First, one player generates an ordered ‘deck’ of cards — the integers (0, 1, 2, 3, …, 51) — and encrypts each one using known randomness. Since this player might be a cheater, she publishes all of her work so the group can repeat and verify it. If all goes well, the group should be confident that the deck is well-formed, i.e., there are no missing cards or duplicates.

Shuffle. The players now pass the deck around the ‘table’, giving each individual a chance to shuffle it thoroughly. This is harder than it sounds; it’s not enough to simply permute the order of the encrypted cards, since the ciphertexts themselves are recognizable (think of each card as having a different back-face). The good news is that schemes like Elgamal allow you to re-randomize a ciphertext — change its outward appearance without changing the underlying plaintext.

Unfortunately, re-randomizing ciphertexts leads to yet another serious limitation: if the output of the shuffle can’t be linked to the input, then a malicious player could simply replace the cards instead of shuffling them. The last player to shuffle would essentially be deciding the order (and even the types of cards in) the deck!

Fortunately, in their quest for better ways to play poker, cryptographers have solved this this problem as well. The answer is something called a publicly-verifiable shuffle (used in Mix networks, which completely by accident were later shown to have applications in e-Voting and anonymous communication). In these systems, the shuffler can actually prove that the shuffled deck contains the same cards, without giving away the shuffle.

Dealing. If everything’s gone well, and if at least one player is honest, the players should now have a beautifully shuffled deck of encrypted cards. It remains only to deal them. To do this, the players cooperatively decrypt the cards using their key shares. If the card is face-up, they go ‘all the way’ and simply reveal the plaintext to the whole group. If it’s face-down, they collaborate most of the way, but let the recipient handle the last component of the decryption process.

Ok, maybe this wasn’t so simple. And there’s still a lot I’m leaving out — including the whole Mix mechanism and a bunch of zero-knowledge proofs you’d need to prevent cheating in the decryption process. Still, figuring that stuff out isn’t the problem.

The problem is that the protocol above is expensive.

A single shuffle alone can result in megabytes of data, which every party has to verify. So much for playing mental poker over the phone (or, to use a modern analogy, Twitter). Clearly a better approach is needed.

Golle to the rescue?

The problem with the ‘classic’ approach is that it requires the players to generate and shuffle an entire deck of cards every time they play. But this is pointless work, since many games don’t actually use the entire deck. A better approach would generate random cards on the fly, then check for ‘collisions’: cards that have already been dealt to the players.

This is what Philippe Golle proposed back in 2005, in a paper submitted to the ITCC e-Gaming track (What is this? It sounds awesome.) I know about this paper because a student recently implemented it in Charm; hence I can attest to the fact that it’s practical. Actually, it cooks.

Golle’s idea was to use the additively-homomorphic property of schemes such as Elgamal,* to allow the parties to draw random cards. In a nutshell, each of the k players selects a random value r in the range 0 to 51, then encrypts her value and publishes it to the other players. The group can now add the ciphertexts together, which gives them the encryption of (r_1 + r_2 + … + r_k).

By working together the group can decrypt the summed ciphertext, which reveals a plaintext in the range 0 to (k*51). By reducing this modulo 52 they obtain a random card number.

The big obstacle to this approach is that you can get repeated cards, i.e., collisions. The clever part of Golle’s protocol is the way that he checks that a given card hasn’t been dealt to a player already, which allows him to ‘throw back’ any colliding cards.

I won’t spend much time on how this works, except to point out that Golle’s paper may have a small bug (though one that’s easily fixed). To make a long story short, when a collision occurs in the first round of dealing — i.e., a card is dealt that already exists in a player’s hand — Golle will actually ‘throw back’ both the new card, and the card that was already in the player’s hand.

Why am I complaining about this? Well, imagine that a real poker dealer did this. That is, he paused, asked to look at your hand, took away the King of Hearts and put it back in the deck (with a brief apology for his mistake). It strikes me that this would not be viewed as kosher. I’ll leave it to a real poker player to tell me what the implications are, but I’m trusting they’re not good.

All the rest

This has been a long post, and while I hope it’s given some of the flavor of the problem, obviously there’s still tons I haven’t said.

For example, how do you check for winning conditions? How do you handle players who ‘drop out’ when the cards don’t go their way? And finally, how would you tie the result of the game to a Bitcoin ‘pot’? (Bitcoin script seems like a great candidate for this, but unfortunately it’s not well supported on the actual Bitcoin network.)

And of course, none of this addresses the real problem with online poker, which mere cryptography does not solve — namely, how to keep your opponents from sharing their hands via a backchannel.

Still, this is a fun area that I’d love to see pursued with a bit more vigor. Yes, from time to time someone promises to do it, but those promises never quite materialize. So if you’re a poker fan and you find this stuff interesting, please do drop me a line.

Notes:

* For the super-wonky, Elgamal is actually multiplicatively homomorphic, but that’s ok. What’s being encrypted is g^r, for some generator g. The product of (g^r1 * g^r2 = g^{r1+r2}) which can be decrypted by testing the result against a table of pre-computed values. (This only works for small values).

Why Antisec matters

A couple of weeks ago the FBI announced the arrest of five members of the hacking group LulzSec. We now know that these arrests were facilitated by ‘Anonymous’ leader* “Sabu“, who, according to court documents, was arrested and ‘turned’ in June of 2011. He spent the next few months working with the FBI to collect evidence against other members of the group.

This revelation is pretty shocking, if only because Anonymous and Lulz were so productive while under FBI leadership. Their most notable accomplishment during this period was the compromise of Intelligence analysis firm Stratfor — culminating in that firm’s (rather embarrassing) email getting strewn across the Internet.

This caps off a fascinating couple of years for our field, and gives us a nice opportunity to take stock. I’m neither a hacker nor a policeman, so I’m not going to spend much time why or the how. Instead, the question that interests me is: what impact have Lulz and Anonymous had on security as an industry?

Computer security as a bad joke

To understand where I’m coming from, it helps to give a little personal background. When I first told my mentor that I was planning to go back to grad school for security, he was aghast. This was a terrible idea, he told me. The reality, in his opinion, was that security was nothing like Cryptonomicon. It wasn’t a developed field. We were years away from serious, meaningful attacks, let alone real technologies that could deal with them.

This seemed totally wrong to me. After all, wasn’t the security industry doing a bazillion dollars of sales ever year? Of course people took it seriously. So I politely disregarded his advice and marched off to grad school — full of piss and vinegar and idealism. All of which lasted until approximately one hour after I arrived on the floor of the RSA trade show. Here I learned that (a) my mentor was a lot smarter than I realized, and (b) idealism doesn’t get you far in this industry.

Do you remember the first time you met a famous person, and found out they were nothing like the character you admired? That was RSA for me. Here I learned that all of the things I was studying in grad school, our industry was studying too. And from that knowledge they were producing a concoction that was almost, but not quite, entirely unlike security.

Don’t get me wrong, it was a rollicking good time. Vast sums of money changed hands. Boxes were purchased, installed, even occasionally used. Mostly these devices were full of hot air and failed promises, but nobody really cared, because after all: security was kind of a joke anyway. Unless you were a top financial services company or (maybe) the DoD, you only really spent money on it because someone was forcing you to (usually for compliance reasons). And when management is making you spend money, buying glossy products is a very effective way to convince them that you’re doing a good job.

Ok, ok, you think I’m exaggerating. Fair enough. So let me prove it to you. Allow me to illustrate my point with a single, successful product, one which I encountered early on in my career. The product that comes to mind is the Whale Communications “e-Gap“, which addressed a pressing issue in systems security, namely: the need to put an “air gap” between your sensitive computers and the dangerous Internet.

Now, this used to be done (inexpensively) by simply removing the network cable. Whale’s contribution was to point out a major flaw in the old approach: once you ‘gap’ a computer, it no longer has access to the Internet!

Hence the e-Gap, which consisted of a memory unit and several electronic switches. These switches were configured such that the memory could be connected only to the Internet or to your LAN, but never to both at the same time (seriously, it gives me shivers). When data arrived at one network port, the device would load up with application data, then flip ‘safely’ to the other network to disgorge its payload. Isolation achieved! Air. Gap.

(A few pedants — damn them — will try to tell you that the e-Gap is a very expensive version of an Ethernet cable. Whale had a ready answer to this, full of convincing hokum about TCP headers and bad network stacks. But really, this was all beside the point: it created a freaking air gap around your network! This apparently convinced Microsoft, who later acquired Whale for five times the GDP of Ecuador.)

Now I don’t mean to sound too harsh. Not all security was a joke. There were plenty of solid companies doing good work, and many, many dedicated security pros who kept it from all falling apart.

But there are only so many people who actually know about security, and as human beings these people are hard to market. To soak up all that cybersecurity dough you needed a product, and to sell that product you needed marketing and sales. And with nobody actually testing vendors’ claims, we eventually wound up with the same situation you get in any computing market: people buying garbage because the booth babes were pretty.**

Lulz, Anonymous and Antisec

I don’t remember when I first heard the term ‘Antisec’, but I do remember what went through my mind at the time: either this is a practical joke, or we’d better harden our servers.

Originally Antisec referred to the ‘Antisec manifesto‘, a document that basically declared war on the computer security industry. The term was too good to be so limited, so LulzSec/Anonymous quickly snarfed it up to refer to their hacking operation (or maybe just part of it, who knows). Wherever the term came from, it basically had one meaning: let’s go f*** stuff up on the Internet.

Since (per my expanation above) network security was pretty much a joke at this point, this didn’t look like too much of a stretch.

And so a few isolated griefing incidents gradually evolved into serious hacking. It’s hard to say where it really got rolling, but to my eyes the first serious casualty of the era was HBGary Federal, who — to be completely honest — were kind of asking for it. (Ok, I don’t mean that. Nobody deserves to be hacked, but certainly if you’re shopping around a plan to ‘target’ journalists and civilians you’d better have some damned good security.)

In case you’re not familiar with the rest of the story, you can get a taste of it here and here. In most cases Lulz/Anonymous simply DDoSed or defaced websites, but in other cases they went after email, user accounts, passwords, credit cards, the whole enchilada. Most of these ‘operations’ left such a mess that it’s hard to say for sure which actually belonged to Anonymous, which were criminal hacks, and which (the most common case) were a little of each.

The bad

So with the background out of the way, let’s get down to the real question of this post. What has all of this hacking meant for the security industry?

Well, obviously, one big problem is that it’s making us (security folks) look like a bunch of morons. I mean, we’ve spent the last N years developing secure products and trying to convince people if they just followed our advice they’d be safe. Yet when it comes down to it, a bunch of guys on the Internet are walking right through it.

This is because for the most part, networks are built on software, and software is crap. You can’t fix software problems by buying boxes, any more than, say, buying cookies will fix your health and diet issues. The real challenge for industry is getting security into the software development process itself — or, even better, acknowledging that we never will, and finding a better way to do things. But this is expensive, painful, and boring. More to the point, it means you can’t outsource your software development to the lowest bidder anymore.

Security folks mostly don’t even try to address this. It’s just too hard. When I ask my software security friends why their field is so terrible (usually because they’re giving me crap about crypto), they basically look at me like I’m from Mars. The classic answer comes from my friend Charlie Miller, who has a pretty firm view of what is, and isn’t his responsibility:

I’m not a software developer, I just break software! If they did it right, I’d be out of a job.

So this is a problem. But beyond bad software, there’s just a lot of rampant unseriousness in the security industry. The best (recent) example comes from RSA, who apparently forgot that their SecurID product was actually important, and decided to make the master secret database accessible from a single compromised Windows workstation. The result of this ineptitude was a series of no-joking-around breaches of US Defense Contractors.

While this has nothing to do with Anonymous, it goes some of the way to explaining why they’ve had such an easy time these past two years.

The good

Fortunately there’s something of a silver lining to this dark cloud. And that is, for once, people finally seem to be taking security seriously. Sort of. Not enough of them, and maybe not in the ways that matter (i.e., building better consumer products). But at least institutionally there seems to be a push away from the absolute stupid.

There’s also been (to my eyes) a renewed interest in data-at-rest encryption, a business that’s never really taken off despite its obvious advantages. This doesn’t mean that people are buying good encryption products (encrypted hard drives come to mind), but at least there’s movement.

To some extent this is because there’s finally something to be scared of. Executives can massage data theft incidents, and payment processors can treat breaches as a cost of doing business, but there’s one thing that no manager will ever stop worrying about. And that is: having their confidential email uploaded to a convenient, searchable web platform for the whole world to see.

The ugly

The last point is that Antisec has finally drawn some real attention to the elephant in the room, namely, the fact that corporations are very bad at preventing targeted breaches. And that’s important because targeted breaches are happening all the time. Corporations mostly don’t know it, or worse, prefer not to admit it.

The ‘service’ that Antisec has provided to the world is simply their willingness to brag. This gives us a few high-profile incidents that aren’t in stealth mode. Take them seriously, since my guess is that for every one of these, there are ten other incidents that we never hear about.***

In Summary

Let me be utterly clear about one thing: none of what I’ve written above should be taken as an endorsement of Lulz, Anonymous, or the illegal defacement of websites. Among many other activities, Anonymous is accused of hacking griefing the public forums of the Epilepsy Foundation of America in an attempt to cause seizures among in its readers. Stay classy, guys.

What I am trying to point out is that something changed a couple of years ago when these groups started operating. It’s made a difference. And it will continue to make a difference, provided that firms don’t become complacent again.

So in retrospect, was my mentor right about the field of information security? I’d say the jury’s still out. Things are moving fast, and they’re certainly interesting enough. I guess we’ll just have to wait and see where it all goes. In the meantime I can content myself with the fact that I didn’t take his alternative advice — to go study Machine Learning. After all, what in the world was I ever going to do with that?

Notes:

* Yes, there are no leaders. Blah blah blah.

** I apologize here for being totally rude and politically incorrect. I wish it wasn’t true.

*** Of course this is entirely speculation. Caveat Emptor.

How do Interception Proxies fail?

I have some substantive posts in the works, but mostly this week hasn’t been good for blogging. In the meantime, I wanted to point readers to this fascinating talk by researcher Jeff Jarmoc, which I learned about through the Corelan team blog:

SSL/TLS Interception Proxies and Transitive Trust

SSL/TLS is entrusted with securing many of the communications services we take for granted in our connected world. Threat actors are also aware of the advantages offered by encrypted communication channels, and increasingly utilize encryption for exploit delivery, malware command-and-control and data exfiltration.

To counter these tactics, organizations are increasingly deploying security controls that intercept end-to-end SSL/TLS channels. Web proxies, DLP systems, specialized threat detection solutions, and network IPSs now offer functionality to intercept, inspect and filter encrypted traffic. Similar functionality is also present in lawful intercept systems and solutions enabling the broad surveillance of encrypted communications by governments. Broadly classified as “SSL/TLS Interception Proxies,” these solutions act as man-in-the-middle, violating the end-to-end security guarantees promised by SSL/TLS.

In this presentation we’ll explore a phenomenon known as “transitive trust,” and explain how deployment of SSL/TLS interception solutions can introduce new vulnerabilities. We detail a collection of new vulnerabilities in widely used interception proxies first discovered by the Dell SecureWorks CTU and responsibly disclosed to the impacted vendors. These vulnerabilities enable attackers to more easily intercept and modify secure communications. In addition, we will introduce a public web site that organizations can use to quickly and easily test for these flaws.

I can’t find Jeff’s slides or whitepaper at the moment (Update: The slides are now public. There’s a lot more to his talk than I cover in this post.) What I can tell from the summary is that Jeff is doing us all an invaluable favor — essentially, putting his hands deep in the scuzz to find out what’s down there.

To make a long story short, the answer is nothing good. The details are in the Corelan post (which, ironically, gives me a TLS error), but to sum it up: Jeff mostly focuses on what interception proxies do when the proxy receives an invalid certificate from a remote website — for example, one that is expired or revoked.

Normally your browser would be the one dealing with this, but in a MITM scenario you’re totally dependent on the proxy. Even if the proxy checks the certificate properly in the first place, they’re still in a tough place. They essentially have the following options:

Reject the connection altogether (probably safest)
Give users the option to proceed or abort (no worse than standard TLS)
Ignore the errors and make the connection anyway (run for the hills!)

Jeff correctly points out that option (3) is the most dangerous, since it opens users up to all kinds of bad TLS connections that would normally ring alarm bells in your browser. Worse, this seems to be the default policy of a number of commercial interception proxies, mostly for unintentional/stupid reasons.

Beyond these default settings, it seems to be that there’s another question here, namely: how are these devices being configured in the field? My guess is that this depends greatly on whether the “victims” of interception know that their TLS traffic is being monitored. If deployers choose to do interception quietly, it could make a big difference in how a proxy will handle cert issues.

I stress that we’re now speculating, but let’s pretend that ACME corporation wants to intercept its employees’ TLS connections, but doesn’t actively want to advertise this fact.* This may restrict their options. For one thing, option (2) is probably out, since this would produce obvious messages on the end-users’ web browser. Even option (1) might be iffy, since some sites will simply not work, without any decent explanation. Hence — in speculation land — one could imagine some organizations deliberately choosing option (3), on the theory that being quiet is better than being secure.**

This is different than the vulnerabilities that Jeff addresses (which mainly deal with devices’ default settings), but it’s something I’ve been wondering about since I first heard of the practice. After all, you’ve gone to all this trouble to get a publicly-rooted MITM CA, now you’re going to advertise that you’re using it? Maybe, maybe not.

The world of TLS MITM interception is a fascinating one, and I can’t possibly learn enough about it. Hopefully we’ll soon learn even more, at least about the nasty CA-facilitated variant of it, as CAs start to respond to Mozilla’s recent ultimatum.

Notes:

* They may notify their employees somehow, but that’s different from reminding them on a daily basis. This isn’t totally nuts: it’s one speculative reason for deploying CA-generated MITM certificates, rather than generating an org certificate and installing it throughout your enterprise.

** I suppose there are workarounds for this case, such as re-writing the MITM cert to include the same class of errors (expiration dates, name errors) but I’d be utterly shocked if anyone uses them.

Surviving a bad RNG

A couple of weeks ago I wrote a long post about random number generation, which I find to be one of the most fascinating subjects in cryptography — mostly because of how terrible things get when people screw it up.

And oh boy, do people screw it up. Back in 2008 it was Debian, with their ‘custom’ OpenSSL implementation that could only produce 32,768 possible TLS keys (do you really need more?) In 2012 it’s 25,000 factorable TLS public keys, all of which appear to have been generated by embedded devices with crappy RNGs.

When this happens, people get nervous. They start to wonder: am I at risk? And if so, what can I do to protect myself?

Answering this question is easy. Answering it in detail is hard. The easy answer is that if you really believe there’s a problem with your RNG, stop reading this blog and go fix it!

The more complicated answer is that many bad things can happen if your RNG breaks down, and some are harder to deal with than others.

In the rest of this post I’m going to talk about this, and give a few potential mitigations. I want to stress that this post is mostly a thought-exercise. Please do not re-engineer OpenSSL around any of the ‘advice’ I give herein (I’m looking at you, Dan Kaminsky), and if you do follow any of my advice, understand the following:

When it all goes terribly wrong, I’ll quietly take down this post and pretend I never wrote it.

In other words, proceed at your own risk. First, some background.

What’s a ‘bad RNG’?

Before we get started, it’s important to understand what it means for an RNG to be broken. In general, failure comes in three or four different flavors, which may or may not share the same root cause:

Predictable output. This usually happens when a generator is seeded with insufficient entropy. The result is that the attacker can actually predict, or at least guess, the exact bits that the RNG will output. This has all kinds of implications, none of them good.
Resetting output. This can occur when a generator repeatedly outputs the same stream of bits, e.g., every time the system restarts. When an attacker deliberately brings about this condition, we refer to it as a Reset Attack, and it’s a real concern for devices like smartcards.
Shared output. Sometimes exactly the same bits will appear on two or more different devices. Often the owners won’t have any idea this is happening until someone else turns up with their public key! This is almost always caused by some hokey entropy source or hardcoded seed value.

These aren’t necessarily distinct problems, and they can easily bleed into one another. For example, a resetting RNG can become a predictable RNG once the adversary observes the first round of outputs. Shared output can become predictable if the attacker gets his hands on another device of the same model. The Debian bug, for example, could be classified into all three categories.

In addition to the problems above, there’s also a fourth (potential) issue:

4. Non-uniform or biased output. It’s at least possible that the output of your generator will exhibit biased outputs, or strings of repeated characters (the kind of thing that tests like DIEHARD look for). In the worst case, it might just start outputting zero bytes.

The good news is that this is relatively unlikely as long as you’re using a standard crypto library. That’s because modern systems usually process their collected entropy through a pseudo-random generator (PRG) built from a hash function or a block cipher.

The blessing of a PRG is that it will usually give you nice, statistically-uniform output even when you feed it highly non-uniform seed entropy. This helps to prevent attacks (like this one) which rely on the presence of obvious biases in your nonces/keys/IVs. While this isn’t a rule, most common RNG failures seem to be related to bad entropy, not to some surprise failure of the PRG.

Unfortunately, the curse is that a good PRG can hide problems. Since most people only see the output of their PRG (rather than the seed material), it’s easy to believe that your RNG is doing a great job, even when it’s actually quite sick.* This has real-world implications: many standards (like FIPS-140) perform continuous tests on the final RNG/PRG output (e.g., for repeated symbols). The presence of a decent PRG renders these checks largely useless, since they’ll really only detect the most catastrophic (algorithmic) failures.

Key generation

When it comes to generating keys with a bad (P)RNG, the only winning move is not to play. Algorithm aside, if an attacker can predict your ‘randomness’, they can generate the same key themselves. Game over. Incidentally, this goes for ephemeral keys as well, meaning that protocols like Diffie-Hellman are not secure in the presence of a predictable RNG (on either side).

If you think there’s any chance this will happen to you, then either (a) generate your keys on a reliable device, or (b) get yourself a better RNG. If neither option is available, then for god’s sake, collect some entropy from the user before you generate keys. Ask them to tap a ditty on a button, or (if a keyboard is available), get a strong, unpredictable passphrase and hash it through PBKDF2 to get a string of pseudo-random bits. This might not save you, but it’s probably better than the alternative.

What’s fascinating is that some cryptosystems are more vulnerable to bad, or shared randomness than others. The recent batch of factorable RSA keys, for example, appears to be the product of poor entropy on embedded devices. But the keys weren’t broken because someone guessed the entropy that was used. Rather, the mere fact that two different devices share entropy was enough to make both of their keys factorable.

According to Nadia Heninger, this is an artifact of the way that RSA keys are generated. Every RSA public modulus is the product of two primes. Some devices generate one prime, then reseed their RNG (with the time, say) before generating the second. The result is two different moduli, each sharing one prime. Unfortunately, this is the worst thing you can do with an RSA key, since anyone can now compute the GCD and efficiently factor both keys.

Although you’re never going to be safe when two devices share entropy, it’s arguable that you’re better off if they at least generate the same RSA key, rather than two moduli with a single shared prime. One solution is to calculate the second prime as a mathematical function of the first. An even easier fix is just to make sure that you don’t reseed between the two primes.

Of course it’s not really fair to call these ‘solutions’. Either way you’re whistling past the graveyard, but at least this might let you whistle a bit longer.

Digital signatures and MACs

There’s a widely held misconception that digital signatures must be randomized. This isn’t true, but it’s understandable that people might think this, since it’s a common property of the signatures we actually use. Before we talk about this, let me stipulate that what we’re talking about here is the signing operation itself — I’m premising this discussion on the very important assumption that we have properly-generated keys.

MACs. The good news is that virtually every practical MAC in use today is deterministic. While there are probabilistic MACs, they’re rarely used. As long as you’re using a standard primitive like HMAC, that bad RNG shouldn’t affect your ability to authenticate your messages.

Signatures. The situation with signatures is a bit more complicated. I can’t cover all signatures, but let’s at least go over the popular ones. For reasons that have never been adequately explored, these are (in no particular order): ECDSA, DSA, RSA-PKCS#1v1.5 and RSA-PSS. Of these four signatures, three are randomized.

The major exception is RSA-PKCS#1v1.5 signature padding, which has no random fields at all. While this means you can give your RNG a rest, it doesn’t mean that v1.5 padding is good. It’s more accurate to say that the ‘heuristically-secure’ v1.5 padding scheme remains equally bad whether you have a working RNG or not.

If you’re signing with RSA, a much better choice is to use RSA-PSS, since that scheme actually has a reduction to the hardness of the RSA problem. So far so good, but wait a second: doesn’t the P in PSS stand for Probabilistic? And indeed, a close look at the PSS description (below) reveals the presence of random salt in every signature.

The good news is that this salt is only an optimization. It allows the designers to obtain a tighter reduction to the RSA problem, but the security proof holds up even if you repeat the salt, or just hardcode it to zero.

The PSS signing algorithm. MGF is constructed from a hash function.

Having dispensed with RSA, we can get down to the serious offenders: DSA and ECDSA.

The problem in a nutshell is that every (EC)DSA signature includes a random nonce value, which must never be repeated. If you ever forget this warning — i.e., create two signatures (on different messages) using the same nonce — then anyone can recover your secret key. This is both easy to detect, and to compute. You could write a script to troll the Internet for repeated nonces (e.g., in X509 certificates), and then outsource the final calculation to a bright eighth-grader.

Usually when DSA/ECDSA go wrong, it’s because someone simply forgot to generate a random nonce in the first place. This appears to be what happened with the Playstation 3. Obviously, this is stupid and you shouldn’t do it. But no matter how careful your implementation, you’re always going to be vulnerable if your RNG starts spitting out repeated values. If this happens to you even once, you need to throw away your key and generate a new one.

There are basically two ways to protect yourself:

Best: don’t to use (EC)DSA in the first place. It’s a stupid algorithm with no reasonable security proof, and as a special bonus it goes completely pear-shaped in the presence of a bad RNG. Unfortunately, it’s also a standard, used in TLS and elsewhere, so you’re stuck with it.
Second best: Derive your nonces deterministically from the message and some secret data. If done correctly (big if!), this prevents two messages from being signed with the same nonce. In the extreme case, this approach completely eliminates the need for randomness in (EC)DSA signatures.There are two published proposals that take this approach. The best is Dan Bernstein’s (somewhat complex) EdDSA proposal, which looks like a great replacement for ECDSA. Unfortunately it’s a replacement, not a patch, since EdDSA uses different elliptic curves and is therefore not cross-compatible with existing ECDSA implementations.
Alternatively, Thomas Pornin has a proposal up that simply modifies (EC)DSA by using HMAC to derive the nonces. The best part about Thomas’s proposal is that it doesn’t break compatibility with existing (EC)DSA implementations. I will caution you, however: while Thomas’s work looks reasonable, his proposal is just a draft (and an expired one to boot). Proceed at your own risk.

Encryption

There are various consequences to using a bad RNG for encryption, most of which depend on the scheme you’re using. Once again we’ll assume that the keys themselves are properly-generated. What’s at stake is the encryption itself.

Symmetric encryption. The good news is that symmetric encryption can be done securely with no randomness at all, provided that you have a strong encryption key and the ability to keep state between messages.

An obvious choice is to use CTR mode encryption. Since CTR mode IVs needn’t be unpredictable, you can set your initial IV to zero, then simply make sure that you always hang onto the last counter value between messages. Provided that you never ever re-use a counter value with a given key (even across system restarts) you’ll be fine.**

This doesn’t work with CBC mode, since that actually does require an unpredictable IV at the head of each chain. You can hack around this requirement in various ways, but I’m not going to talk about those here; nothing good will come of it.

Public-key encryption. Unfortunately, public-key encryption is much more difficult to get right without a good RNG.

Here’s the fundamental problem: if an attacker knows the randomness you used to produce a ciphertext, then (in the worst case) she can simply encrypt ‘guess’ messages until she obtains the same ciphertext as you. At that point she knows what you encrypted.***

Obviously this attack only works if the attacker can guess the message you encrypted. Hence it’s possible that high-entropy messages (symmetric keys, for example) will encrypt securely even without good randomness. But there’s no guarantee of this. Elgamal, for example, can fail catastrophically when you encrypt two messages with the same random nonce.****

Although I’m not going to endorse any specific public-key encryption scheme, it seems likely that some schemes will hold up better than others. For example, while predictably-randomized RSA-OAEP and RSA-OAEP+ will both be vulnerable to guessing attacks, there’s some (intuitive) reason to believe that they’ll remain secure for high-entropy messages like keys. I can’t prove this, but it seems like a better bet than using Elgamal (clearly broken) or older padding schemes like RSA-PKCS#1v1.5.

If my intuition isn’t satisfying to you, quite a lot of research is still being done in this area. See for example, recent works on deterministic public-key encryption, or hedged public-key encryption. Note that all of this work makes on the assumption that you’re encrypting high-entropy messages.

Protocols

I can’t conclude this post without at least a token discussion of how a bad RNG can affect cryptographic protocols. The short version is that it depends on the protocol. The shorter version is that it’s almost always bad.

Consider the standard TLS handshake. Both sides use their RNGs to generate nonces. Then the client generates a random ‘Pre-master Secret’ (PMS), encrypts it under the server’s key, and transmits it over the wire. The ‘Master Secret’ (and later, transport key) is derived by hashing together all of the nonces and the PMS.

Since the PMS is the only real ‘secret’ in the protocol (everything else is sent in the clear), predicting it is the same as recovering the transport key. Thus TLS is not safe to use if the client RNG is predictable. What’s interesting is that the protocol is secure (at least, against passive attackers) even if the server’s RNG fails. I can only guess that this was a deliberate choice on the part of TLS’s designers.

SSL handshake (source).

Protocols are already plenty exciting when you have a working RNG. Adding a bad RNG to the mix is like pouring fireworks on a fire. It’s at least possible to build protocols that are resilient to one participant losing their RNG, but it’s very tricky to accomplish — most protocols will fail in unexpected ways.

In Summary

If you take nothing else from this post, I hope it’s this: using a broken RNG is just a bad idea. If you think there’s any chance your generator will stop working, then for god’s sake, fix it! Don’t waste your time doing any of the stuff I mention above.

That said, there legitimately are cases where your RNG can go wrong, or where you don’t have one in the first place. The purpose of this post was to help you understand these scenarios, and the potential consequences for your system. So model it. Think about it. Then spend your time on better things.

Notes:

* The classic example is Debian’s 2008 OpenSSL release, which used a 15-bit process ID as the only seed for its PRG. This wasn’t obvious during testing, since the 32,768 possible RNG streams all looked pretty random. It was only after the public release that people noticed that many devices were sharing TLS keys.

** If you’re going to do this, you should also be sure to use a MAC on your ciphertext, including the initial counter value for each message.

*** A great example is unpadded, textbook RSA. If m is random, then it’s quite difficult to recover m given m^e mod N. If, however, you have a few good guesses for m and you know the public key (N, e), you can easily try each of your guesses and compare the results.

**** Given two Elgamal ciphertexts on the same key and randomness (g^r, y^r*M1), (g^r, y^r*M2) you can easily compute M1/M2. A similar thing happens with hash Elgamal. This may or may not be useful to you, depending on how much you know about the content of the various messages.

A brief update

My early-week post on the MITM certificate mess seems to have struck a nerve with readers. (Or perhaps I just picked the right time to complain!) Since folks seem interested in this subject, I wanted to follow up with a few quick updates:

The EFF has released a new version of HTTPS Everywhere, which includes a nifty ‘Decentralized SSL Observatory’ feature. This scans for unusual certificates (e.g., MITM certs, certs with weak keys) and reports them back to EFF for logging. A very nice step towards a better ‘net.
StalkR reminds me that Chrome 18 includes support for Public-key Pinning. This is an HTTP extension that allows a site operator to ‘pin’ their site to one (or more) pre-specified public keys for a given period of time. A pinned browser will reject any alternative keys that show up — even if they’re embedded in a valid certificate.
A couple of readers point out that popular sites (e.g., Google and Facebook) change their certificates quite frequently — possibly due to the use of load balancers — which poses a problem for “carry a list of legitimate certs with you” solutions. I recognize this. The best I can say is that we’re all better off if bogus certs are easy to detect. Hopefully site operators will find a compromise that makes this easy for us.

Appearances to the contrary, this blog is not going to become a forum for complaining about CAs. I’ll be back in a few days with more wonky crypto posts, including some ideas for dealing with bad randomness, some thoughts on patented modes of operation, and an update on the progress that researchers are making with Fully-Homomorphic Encryption.

The Internet is broken: could we please fix it?

Ok, this is a little embarrassing and I hate having to admit it publicly. But I can’t hold it in any longer: I think I’m becoming an Internet activist.

This is upsetting to me, since active is the last thing I ever thought I’d be. I have friends who live to make trouble for big corporations on the Internet, and while I admire their chutzpah (and results!), they’ve always made me a little embarrassed. Even when I agree with their cause, I still have an urge to follow along, cleaning up the mess and apologizing on behalf of all the ‘reasonable’ folks on the Internet.

But every man has a breaking point, and the proximate cause of mine is Trustwave. Or rather, the news that Trustwave — an important CA and pillar of the Internet — took it upon themselves to sell a subordinate root cert to some (still unknown) client, for the purposes of undermining the trust assumptions that make the Internet secure eavesdropping on TLS connections.

This kind of behavior is absolutely, unquestionably out of bounds for a trusted CA, and certainly deserves a response — a stronger one than it’s gotten. But the really frightening news is twofold:

There’s reason to believe that other (possibly bigger) CAs are engaged in the same practice.
To the best of my knowledge, only one browser vendor has taken a public stand on this issue, and that vendor isn’t gaining market share.

The good news is that the MITM revelation is exactly the sort of kick we’ve needed to improve the CA system. And even better, some very bright people are already thinking about it. The rest of this post will review the problem and talk about some of the potential solutions.

Certificates 101

For those of you who know the TLS protocol (and how certificates work), the following explanation is completely gratuitous. Feel free to skip it. If you don’t know — or don’t understand the problem — I’m going to take a minute to give some quick background.

TLS (formerly SSL) is probably the best-known security protocol on the Internet. Most people are familiar with TLS for its use in https — secure web — but it’s also used to protect email in transit, software updates, and a whole mess of other stuff you don’t even think about.

TLS protects your traffic by encrypting it with a strong symmetric key algorithm like AES or RC4. Unfortunately, this type of cryptography only works when the communicating parties share a key. Since you probably don’t share keys with most of the web servers on the Internet, TLS provides you with a wonderful means to do so: a public-key key agreement protocol.

I could spend a lot of time talking about this, but for our purposes, all you need to understand is this: when I visit https://gmail.com, Google’s server will send me a public key. If this key really belongs to Google, then everything is great: we can both derive a secure communication key, even if our attacker Mallory is eavesdropping on the whole conversation.

If, on the other hand, Mallory can intercept and modify our communications, the game is very different. In this case, she can overwrite Gmail’s key with her own public key. The result: I end up sharing a symmetric key with her! The worst part is that I probably won’t know this has happened: clever Mallory can make her own connection to Gmail and silently pass my traffic through — while reading every word. This scenario is called a Man in the Middle (MITM) Attack.

MITM attack. Alice is your grandfather, Bob is BankofAmerica.com, and Mallory establishes connections with both. (Wikipedia/CC license)

MITM attacks are older than the hills. Fortunately TLS has built-in protections to thwart them. Instead of transmitting a naked public key, the Gmail server wraps its key in a certificate; this is a simple file that embeds both the key and some identifying information, like “gmail.com”. The certificate is digitally signed by someone very trustworthy: one of a few dozen Certificate Authorities (CA) that your browser knows and trusts. These include companies like Verisign, and (yes) Trustwave.

TLS clients (e.g., web browsers) carry the verification keys for a huge number of CAs. When a certificate comes in, they can verify its signature to ensure that it’s legit. This approach works very well, under one very important assumption: namely, Mallory won’t be able to get a signed certificate on a domain she doesn’t own.

What’s wrong with the CA model?

The real problem with the CA model is that every root CA has the power to sign any domain, which completely unravels the security of TLS. So far the industry has policed itself using the Macaroni Grill model: If a CA screws up too badly, they face being removed from the ‘trusted’ list of major TLS clients. In principle this should keep people in line, since it’s the nuclear option for a CA — essentially shutting down their business.

Unfortunately while this sounds good it’s tricky to implement in practice. That’s because:

It assumes that browser vendors are willing to go nuclear on their colleagues at the CAs.
It assumes that browser vendors can go nuclear on a major CA, knowing that the blowback might very well hurt their product. (Imagine that your browser unilaterally stopped accepting Verisign certs. What would you do?)
It assumes that someone will catch misbehaving CAs in the first place.

What’s fascinating about the Trustwave brouhaha is that it’s finally giving us some visibility into how well these assumptions play out in the real world.

So what happened with Trustwave?

In late January of this year, Trustwave made a cryptic update to their CA policy. When people started asking about it, they responded with a carefully-worded post on the company blog. When you cut through the business-speak, here’s what it says:

We sold the right to generate certificates — on any domain name, regardless of whether it belongs to one of our clients or not — and packed this magical capability into a box. We rented this box to a corporate client for the express purpose of running Man-in-the-Middle attacks to eavesdrop on their employees’ TLS-secured connections. At no point did we stop to consider how damaging this kind of practice was, nor did we worry unduly about its potential impact on our business — since quite frankly, we didn’t believe it would have any.

I don’t know which part is worse. That a company whose entire business is based on trust — on the idea that people will believe them when they say a certificate is legit — would think they could get away with selling a tool to make fraudulent certificates. Or that they’re probably right.

But this isn’t the worst of it. There’s reason to believe that Trustwave isn’t alone in this practice. In fact, if we’re to believe the rumors, Trustwave is only noteworthy in that they stopped. Other CAs may still be up to their ears.

And so this finally brings us to the important part of this post: what’s being done, and what can we do to make sure that it never happens again?

Option 1: Rely on the browser vendors

What’s particularly disturbing about the Trustwave fiasco is the response it’s gotten from the various browser manufacturers.

So far exactly one organization has taken a strong stand against this practice. The Mozilla foundation (makers of Firefox) recently sent a strongly-worded letter to all of their root CAs — demanding that they disclose whether such MITM certificates exist, and that they shut them down forthwith. With about 20% browser share (depending on who’s counting), Mozilla has the means to enforce this. Assuming the vendors are honest, and assuming Mozilla carries through on its promise. And assuming that Mozilla browser-share doesn’t fall any further.

That’s the good news. Less cheerful is the deafening silence from Apple, Microsoft and Google. These vendors control most of the remaining browser market, and to the best of my knowledge they’ve said nothing at all about the practice. Publicly, anyway. It’s possible that they’re working the issue privately; if so, more power to them. But in the absence of some evidence, I find it hard to take this on faith.

Option 2: Sunlight is the best disinfectant

The Trustwave fiasco exposes two basic problems with the CA model: (1) any CA can claim ownership of any domain, and (2) there’s no easy way to know which domains a CA has put its stamp on.

This last is very much by CA preference: CAs don’t want to reveal their doings, on the theory that it would harm their business. I can see where they’re coming from (especially if their business includes selling MITM certs!) Unfortunately, allowing CAs to operate without oversight is one of those quaint practices (like clicking on links sent by strangers) that made sense in a more innocent time, but no longer has much of a place in our world.

Merkle tree (Wikipedia/CC)

Ben Laurie and Adam Langley feel the same way, and they’ve developed a plan to do something about it. The basic idea is this:

Every new certificate should be published in a public audit log. This log will be open to the world, which means that everyone can scan for illegal entries (i.e., their own domain appearing in somebody else’s certificate.)
Anytime a web server hands out a certificate, it must prove that the certificate is contained in the list.

The beautiful thing is that this proof can be conducted relatively efficiently using a Merkle hash tree. The resulting proofs are quite short (log(N) hashes, where N is the total number of certificates). Browsers will need to obtain the current tree root, which requires either (a) periodic scanning of the tree, or some degree of trust in an authority, who will periodically distribute signed root nodes.

Along the same lines, the EFF has a similar proposal called the Sovereign Keys Project. SKP also proposes a public log, but places stronger requirements on what it takes to get into the log. It’s quite likely that in the long run these projects will merge, or give birth to something even better.

Option 3: Eternal vigilance

The problem with SKP and the Laurie/Langley proposal is that both require changes to the CA infrastructure. Someone will need to construct these audit logs; servers will have to start shipping hash proofs. Both can be incrementally deployed, but will only be effective once deployment reaches a certain level.

Another option is to dispense with this machinery altogether, and deal with rogue CAs today by subjecting them to contant, unwavering surveillance. This is the approach taken by CMU’s Perspectives plugin and by Moxie Marlinspike’s Convergence.

The core idea behind both of these systems is to use ‘network perspectives’ to determine whether the certificate you’re receiving is the same certificate that everyone else is. This helps to avoid MITMs, since presumably the attacker can only be in the ‘middle’ of so many network paths. To accomplish this, both systems deploy servers called Notaries — run on a volunteer basis — which you can call up whenever you receive an unknown certificate. They’ll compare your version of the cert to what they see from the same server, and help you ring the alarm if there’s a mismatch.

A limitation of this approach is privacy; these Notary servers obviously learn quite a bit about the sites you visit. Convergence extends the Perspectives plugin to address some of these issues, but fundamentally there’s no free lunch here. If you’re querying some external party, you’re leaking information.

One solution to this problem is to dispense with online notary queries altogether, and just ask people to carry a list of legitimate certificates with them. If we assume that there are 4 million active certificates in the world, we could easily fit them into a < 40MB Bloom filter. This would allow us to determine whether a cert is ‘on the list’ without making an online query. Of course, this requires someone to compile and maintain such a list. Fortunately there are folks already doing this, including the EFF’s SSL Observatory project.

Option 4: The hypothetical

The existence of these proposals is definitely heartening. It means that people are taking this seriously, and there’s an active technical discussion on how to make things better.

Since we’re in this mode, let me mention a few other things that could make a big difference in detecting exploits. For one thing, it would be awfully nice if web servers had a way to see things through their clients’ eyes. One obvious way to do this is through script: use Javascript to view the current server certificate, and report the details back to the server.

Of course this isn’t perfect — a clever MITM could strip the Javascript or tamper with it. Still, obfuscation is a heck of a lot easier then de-obfuscation, and it’s unlikely that a single attacker is going to win an arms race against a variety of sites.

Unfortunately, this idea has to be relegated to the ‘could be, should be’ dustbin, mostly because Javascript doesn’t have access to the current certificate info. I don’t really see the reason for this, and I sure hope that it changes in the future.

Option 5: The long arm of the law

I suppose the last option — perhaps the least popular — is just to treat CAs the same way that you’d treat any important, trustworthy organization in the real world. That means: you cheat, you pay the penalty. Just as we shouldn’t tolerate Bank of America knowingly opening a credit line in the name of a non-customer, we shouldn’t tolerate a CA doing the same.

Option 6: Vigilante justice

Ok, I’m only kidding about this one, cowboy. You can shut down that LOIC download right now.

In summary

I don’t know that there’s a magical vaccine that will make the the CA system secure, but I’ve come to believe that the current approach is not working. It’s not just examples like Trustwave, which (some might argue) is a relatively limited type of abuse. It’s that the Trustwave revelation comes in addition to a steady drumbeat of news about stolen keys, illegitimately-obtained certificates, and various other abuses.

While dealing with these problems might not be easy, what’s shocking is how easy it would be to at least detect and expose the abuses at the core of it — if various people agreed that this was a worthy goal. I do hope that people start taking this stuff seriously, mostly because being a radical is hard, hard work. I’m just not cut out for it.

Some random thoughts about crypto. Notes from a course I teach. Pictures of my dachshunds.

Semantic Security

Encrypting your own key

Circles and cycles

It gets worse

So what do we do about this?

What the heck is (was) False Start anyway?

False Start sounds awesome: why did Google yank it?

Ok, it has issues. But is it secure?

Hands off my NSS

In summary

Quantum vs. Classical

Quantum computers are not magic!

An algorithm for a computer that doesn’t exist

So what can we do about it?

In summary

The mud puddle test

You wanna make something of it?

But can’t we fix this with Public-Key Encryption/Quantum Cryptography/ESP/Magical Unicorns?

So what is the alternative?

In summary

Secret history

Face up or Face Down?

Golle to the rescue?

All the rest

Computer security as a bad joke

Lulz, Anonymous and Antisec

The bad

The good

The ugly

In Summary

What’s a ‘bad RNG’?

Key generation

Digital signatures and MACs

Encryption

Protocols

In Summary

Certificates 101

What’s wrong with the CA model?

So what happened with Trustwave?

Option 1: Rely on the browser vendors

Option 2: Sunlight is the best disinfectant

Option 3: Eternal vigilance

Option 4: The hypothetical

Option 5: The long arm of the law

Option 6: Vigilante justice

In summary

Menu

**Ok, it has issues. But is it secure?**