 A couple of weeks ago I wrote a long post about random number generation, which I find to be one of the most fascinating subjects in cryptography — mostly because of how terrible things get when people screw it up.
A couple of weeks ago I wrote a long post about random number generation, which I find to be one of the most fascinating subjects in cryptography — mostly because of how terrible things get when people screw it up.
And oh boy, do people screw it up. Back in 2008 it was Debian, with their ‘custom’ OpenSSL implementation that could only produce 32,768 possible TLS keys (do you really need more?) In 2012 it’s 25,000 factorable TLS public keys, all of which appear to have been generated by embedded devices with crappy RNGs.
When this happens, people get nervous. They start to wonder: am I at risk? And if so, what can I do to protect myself?
Answering this question is easy. Answering it in detail is hard. The easy answer is that if you really believe there’s a problem with your RNG, stop reading this blog and go fix it!
The more complicated answer is that many bad things can happen if your RNG breaks down, and some are harder to deal with than others.
In the rest of this post I’m going to talk about this, and give a few potential mitigations. I want to stress that this post is mostly a thought-exercise. Please do not re-engineer OpenSSL around any of the ‘advice’ I give herein (I’m looking at you, Dan Kaminsky), and if you do follow any of my advice, understand the following:
When it all goes terribly wrong, I’ll quietly take down this post and pretend I never wrote it.
In other words, proceed at your own risk. First, some background.
What’s a ‘bad RNG’?
Before we get started, it’s important to understand what it means for an RNG to be broken. In general, failure comes in three or four different flavors, which may or may not share the same root cause:
- Predictable output. This usually happens when a generator is seeded with insufficient entropy. The result is that the attacker can actually predict, or at least guess, the exact bits that the RNG will output. This has all kinds of implications, none of them good.
- Resetting output. This can occur when a generator repeatedly outputs the same stream of bits, e.g., every time the system restarts. When an attacker deliberately brings about this condition, we refer to it as a Reset Attack, and it’s a real concern for devices like smartcards.
- Shared output. Sometimes exactly the same bits will appear on two or more different devices. Often the owners won’t have any idea this is happening until someone else turns up with their public key! This is almost always caused by some hokey entropy source or hardcoded seed value.
These aren’t necessarily distinct problems, and they can easily bleed into one another. For example, a resetting RNG can become a predictable RNG once the adversary observes the first round of outputs. Shared output can become predictable if the attacker gets his hands on another device of the same model. The Debian bug, for example, could be classified into all three categories.
In addition to the problems above, there’s also a fourth (potential) issue:
4. Non-uniform or biased output. It’s at least possible that the output of your generator will exhibit biased outputs, or strings of repeated characters (the kind of thing that tests like DIEHARD look for). In the worst case, it might just start outputting zero bytes.
The good news is that this is relatively unlikely as long as you’re using a standard crypto library. That’s because modern systems usually process their collected entropy through a pseudo-random generator (PRG) built from a hash function or a block cipher.
The blessing of a PRG is that it will usually give you nice, statistically-uniform output even when you feed it highly non-uniform seed entropy. This helps to prevent attacks (like this one) which rely on the presence of obvious biases in your nonces/keys/IVs. While this isn’t a rule, most common RNG failures seem to be related to bad entropy, not to some surprise failure of the PRG.
Unfortunately, the curse is that a good PRG can hide problems. Since most people only see the output of their PRG (rather than the seed material), it’s easy to believe that your RNG is doing a great job, even when it’s actually quite sick.* This has real-world implications: many standards (like FIPS-140) perform continuous tests on the final RNG/PRG output (e.g., for repeated symbols). The presence of a decent PRG renders these checks largely useless, since they’ll really only detect the most catastrophic (algorithmic) failures.
Key generation
When it comes to generating keys with a bad (P)RNG, the only winning move is not to play. Algorithm aside, if an attacker can predict your ‘randomness’, they can generate the same key themselves. Game over. Incidentally, this goes for ephemeral keys as well, meaning that protocols like Diffie-Hellman are not secure in the presence of a predictable RNG (on either side).
If you think there’s any chance this will happen to you, then either (a) generate your keys on a reliable device, or (b) get yourself a better RNG. If neither option is available, then for god’s sake, collect some entropy from the user before you generate keys. Ask them to tap a ditty on a button, or (if a keyboard is available), get a strong, unpredictable passphrase and hash it through PBKDF2 to get a string of pseudo-random bits. This might not save you, but it’s probably better than the alternative.
What’s fascinating is that some cryptosystems are more vulnerable to bad, or shared randomness than others. The recent batch of factorable RSA keys, for example, appears to be the product of poor entropy on embedded devices. But the keys weren’t broken because someone guessed the entropy that was used. Rather, the mere fact that two different devices share entropy was enough to make both of their keys factorable.
According to Nadia Heninger, this is an artifact of the way that RSA keys are generated. Every RSA public modulus is the product of two primes. Some devices generate one prime, then reseed their RNG (with the time, say) before generating the second. The result is two different moduli, each sharing one prime. Unfortunately, this is the worst thing you can do with an RSA key, since anyone can now compute the GCD and efficiently factor both keys.
Although you’re never going to be safe when two devices share entropy, it’s arguable that you’re better off if they at least generate the same RSA key, rather than two moduli with a single shared prime. One solution is to calculate the second prime as a mathematical function of the first. An even easier fix is just to make sure that you don’t reseed between the two primes.
Of course it’s not really fair to call these ‘solutions’. Either way you’re whistling past the graveyard, but at least this might let you whistle a bit longer.
Digital signatures and MACs
There’s a widely held misconception that digital signatures must be randomized. This isn’t true, but it’s understandable that people might think this, since it’s a common property of the signatures we actually use. Before we talk about this, let me stipulate that what we’re talking about here is the signing operation itself — I’m premising this discussion on the very important assumption that we have properly-generated keys.
MACs. The good news is that virtually every practical MAC in use today is deterministic. While there are probabilistic MACs, they’re rarely used. As long as you’re using a standard primitive like HMAC, that bad RNG shouldn’t affect your ability to authenticate your messages.
Signatures. The situation with signatures is a bit more complicated. I can’t cover all signatures, but let’s at least go over the popular ones. For reasons that have never been adequately explored, these are (in no particular order): ECDSA, DSA, RSA-PKCS#1v1.5 and RSA-PSS. Of these four signatures, three are randomized.
The major exception is RSA-PKCS#1v1.5 signature padding, which has no random fields at all. While this means you can give your RNG a rest, it doesn’t mean that v1.5 padding is good. It’s more accurate to say that the ‘heuristically-secure’ v1.5 padding scheme remains equally bad whether you have a working RNG or not.
If you’re signing with RSA, a much better choice is to use RSA-PSS, since that scheme actually has a reduction to the hardness of the RSA problem. So far so good, but wait a second: doesn’t the P in PSS stand for Probabilistic? And indeed, a close look at the PSS description (below) reveals the presence of random salt in every signature.
The good news is that this salt is only an optimization. It allows the designers to obtain a tighter reduction to the RSA problem, but the security proof holds up even if you repeat the salt, or just hardcode it to zero.
 |
| The PSS signing algorithm. MGF is constructed from a hash function. |
Having dispensed with RSA, we can get down to the serious offenders: DSA and ECDSA.
The problem in a nutshell is that every (EC)DSA signature includes a random nonce value, which must never be repeated. If you ever forget this warning — i.e., create two signatures (on different messages) using the same nonce — then anyone can recover your secret key. This is both easy to detect, and to compute. You could write a script to troll the Internet for repeated nonces (e.g., in X509 certificates), and then outsource the final calculation to a bright eighth-grader.
Usually when DSA/ECDSA go wrong, it’s because someone simply forgot to generate a random nonce in the first place. This appears to be what happened with the Playstation 3. Obviously, this is stupid and you shouldn’t do it. But no matter how careful your implementation, you’re always going to be vulnerable if your RNG starts spitting out repeated values. If this happens to you even once, you need to throw away your key and generate a new one.
There are basically two ways to protect yourself:
- Best: don’t to use (EC)DSA in the first place. It’s a stupid algorithm with no reasonable security proof, and as a special bonus it goes completely pear-shaped in the presence of a bad RNG. Unfortunately, it’s also a standard, used in TLS and elsewhere, so you’re stuck with it.
- Second best: Derive your nonces deterministically from the message and some secret data. If done correctly (big if!), this prevents two messages from being signed with the same nonce. In the extreme case, this approach completely eliminates the need for randomness in (EC)DSA signatures.There are two published proposals that take this approach. The best is Dan Bernstein’s (somewhat complex) EdDSA proposal, which looks like a great replacement for ECDSA. Unfortunately it’s a replacement, not a patch, since EdDSA uses different elliptic curves and is therefore not cross-compatible with existing ECDSA implementations.
Alternatively, Thomas Pornin has a proposal up that simply modifies (EC)DSA by using HMAC to derive the nonces. The best part about Thomas’s proposal is that it doesn’t break compatibility with existing (EC)DSA implementations. I will caution you, however: while Thomas’s work looks reasonable, his proposal is just a draft (and an expired one to boot). Proceed at your own risk.
Encryption
There are various consequences to using a bad RNG for encryption, most of which depend on the scheme you’re using. Once again we’ll assume that the keys themselves are properly-generated. What’s at stake is the encryption itself.
Symmetric encryption. The good news is that symmetric encryption can be done securely with no randomness at all, provided that you have a strong encryption key and the ability to keep state between messages.
An obvious choice is to use CTR mode encryption. Since CTR mode IVs needn’t be unpredictable, you can set your initial IV to zero, then simply make sure that you always hang onto the last counter value between messages. Provided that you never ever re-use a counter value with a given key (even across system restarts) you’ll be fine.**
This doesn’t work with CBC mode, since that actually does require an unpredictable IV at the head of each chain. You can hack around this requirement in various ways, but I’m not going to talk about those here; nothing good will come of it.
Public-key encryption. Unfortunately, public-key encryption is much more difficult to get right without a good RNG.
Here’s the fundamental problem: if an attacker knows the randomness you used to produce a ciphertext, then (in the worst case) she can simply encrypt ‘guess’ messages until she obtains the same ciphertext as you. At that point she knows what you encrypted.***
Obviously this attack only works if the attacker can guess the message you encrypted. Hence it’s possible that high-entropy messages (symmetric keys, for example) will encrypt securely even without good randomness. But there’s no guarantee of this. Elgamal, for example, can fail catastrophically when you encrypt two messages with the same random nonce.****
Although I’m not going to endorse any specific public-key encryption scheme, it seems likely that some schemes will hold up better than others. For example, while predictably-randomized RSA-OAEP and RSA-OAEP+ will both be vulnerable to guessing attacks, there’s some (intuitive) reason to believe that they’ll remain secure for high-entropy messages like keys. I can’t prove this, but it seems like a better bet than using Elgamal (clearly broken) or older padding schemes like RSA-PKCS#1v1.5.
If my intuition isn’t satisfying to you, quite a lot of research is still being done in this area. See for example, recent works on deterministic public-key encryption, or hedged public-key encryption. Note that all of this work makes on the assumption that you’re encrypting high-entropy messages.
Protocols
I can’t conclude this post without at least a token discussion of how a bad RNG can affect cryptographic protocols. The short version is that it depends on the protocol. The shorter version is that it’s almost always bad.
Consider the standard TLS handshake. Both sides use their RNGs to generate nonces. Then the client generates a random ‘Pre-master Secret’ (PMS), encrypts it under the server’s key, and transmits it over the wire. The ‘Master Secret’ (and later, transport key) is derived by hashing together all of the nonces and the PMS.
Since the PMS is the only real ‘secret’ in the protocol (everything else is sent in the clear), predicting it is the same as recovering the transport key. Thus TLS is not safe to use if the client RNG is predictable. What’s interesting is that the protocol is secure (at least, against passive attackers) even if the server’s RNG fails. I can only guess that this was a deliberate choice on the part of TLS’s designers.
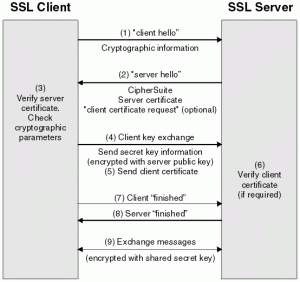 |
| SSL handshake (source). |
Protocols are already plenty exciting when you have a working RNG. Adding a bad RNG to the mix is like pouring fireworks on a fire. It’s at least possible to build protocols that are resilient to one participant losing their RNG, but it’s very tricky to accomplish — most protocols will fail in unexpected ways.
In Summary
If you take nothing else from this post, I hope it’s this: using a broken RNG is just a bad idea. If you think there’s any chance your generator will stop working, then for god’s sake, fix it! Don’t waste your time doing any of the stuff I mention above.
That said, there legitimately are cases where your RNG can go wrong, or where you don’t have one in the first place. The purpose of this post was to help you understand these scenarios, and the potential consequences for your system. So model it. Think about it. Then spend your time on better things.
Notes:
* The classic example is Debian’s 2008 OpenSSL release, which used a 15-bit process ID as the only seed for its PRG. This wasn’t obvious during testing, since the 32,768 possible RNG streams all looked pretty random. It was only after the public release that people noticed that many devices were sharing TLS keys.
** If you’re going to do this, you should also be sure to use a MAC on your ciphertext, including the initial counter value for each message.
*** A great example is unpadded, textbook RSA. If m is random, then it’s quite difficult to recover m given m^e mod N. If, however, you have a few good guesses for m and you know the public key (N, e), you can easily try each of your guesses and compare the results.
**** Given two Elgamal ciphertexts on the same key and randomness (g^r, y^r*M1), (g^r, y^r*M2) you can easily compute M1/M2. A similar thing happens with hash Elgamal. This may or may not be useful to you, depending on how much you know about the content of the various messages.
Hyperlink in “helps to prevent attacks (like this one) which rely on the presence of obvious biases in your nonces/keys/IVs” is broken.
I'm kind of confused about your public-key encryption example. What you're describing is more or less a dictionary attack, right? Can't the attacker mount this attack even if he or she doesn't have any info about your RNG? i.e. The attacker just encrypts random messages using your public key until he gets one that matches?
Most public-key encryption schemes are randomized. This means the encryption algorithm takes in not only the message, but also some random bits (a good example here is the OAEP padding scheme for RSA, which has an explicit random field). If you're using good randomness, then a given message /shouldn't/ encrypt to the same ciphertext ever (or almost ever), which prevents the sort of dictionary/guessing attacks I describe above. For more about this, you can look up “probabilistic encryption” or “semantic security”.
Unfortunately this approach only works when the randomness is unpredictable. If an attacker knows the random bits used to encrypt, then guessing/dictionary attacks are back on the table.
Eric: No, because if the message is properly padded before encryption then the attacker has to correctly guess both the message content *and* the randomised padding.
For amusement try this on openbsd:
#include
#include
int
main (int argc, char *argv[])
{
int i;
srandom (0);
for (i = 0; i < 32; i++)
printf (“%ld\n”, random ());
return 0;
}
Excellent article, thanks for sharing it!
Good informative article, thanks for sharing
tap bolts
> provided that you have a strong encryption key and the ability to keep state between messages
If you have a strong key and the ability to keep persistent state, you can easily construct a decent PRNG from that. The situations where I'd want to guard against a broken PRNG are those were I either don't have a strong per-device key, or I don't trust the state to persist reliably.
For example restoring from backup, cloning VMs,…
In such a situation I'd be more afraid of CTR than of CBC (though both suck without good IVs).
———
There are also some other (weaker) failure modes for a PRNG:
1) Lack of forward secrecy. CTR mode would fail this, OFB would not.
If you learn the internal state of the PRNG at some point, you can compute its past values.
2) Lack of backward secrecy. Needs regular reseeding with fresh entropy.
If you learn the internal state of the PRNG at some point, you can compute its future values.
experiencing some small security problems with my latest blog and I’d like to find something more safeguarded. Do you have any recommendations?
Absolutely pent subject matter, appreciate it for selective information .
Thanks for a very interesting web site. Where else could I get that kind of info written in such an ideal approach? I have a undertaking that I'm just now working on, and I've been at the look out for such information.
agen bola
A great help for me to read. Nobody can screw up your article for it is well-informed on how a bad RNG can affect cryptographic protocols. Thanks a lot!
It is perfect time to make some plans for the future and it is time to be happy. I've read this post and if I could I desire to suggest you some interesting things or suggestions. Perhaps you could write next articles referring to this article. I want to read more things about it!
Jasa SEO