 |
| Unitards: another consequence of quantum computing. |
Back in December I asked readers for some topics they were particularly keen to read about on this blog. One of the best (and sadly, most challenging) suggestions was to say something about post-quantum cryptography. Roughly speaking, this term describes the future of cryptography after quantum computers arrive and screw things up for everyone.
Now, just for the record, quantum computing is not a bad thing; in fact, it’s one of the most exciting discoveries of our time. At minimum QCs will help us efficiently solve challenging problems that take forever on today’s computers. It’s entirely possible, though not guaranteed, that they’ll totally revolutionalize the way we compute (see this breathless article). Whichever it is, quantum computers will be a general good.
But not necessarily for cryptographers.
This is because cryptographers don’t always want faster algorithms for solving hard problems. It isn’t that we thrive on people’s frustration; it’s that many of our best cryptosystems simply depend on the hardness of problems like integer factorization. By making these problems easy, QCs throw a huge wrench into the works. And this isn’t a hypothetical concern: thanks to Shor’s algorithm, many of our most beloved cryptosystems are already living on borrowed time.
But all is not lost. We have two very important things working in our favor. The first is time. For all the excitement around quantum computing, nobody’s managed to actually build a useful one. And (no matter what D-Wave says) it doesn’t look like they will anytime soon.
The second is that quantum computers are not magic. QCs are very good at quickly solving certain problems, but their usefulness is more limited than most people realize. Moreover, we only know of a handful of useful quantum algorithms today. This could change: think how many classical algorithms were discovered after classical computers were built. But it gives us hope.
In the rest of this post I’m going to try to give a flavor of the problem, and point out some of the bright spots — areas where we feel pretty good. I want to be clear that this isn’t my research area, and many of the best ideas in this post come from the excellent book Post-Quantum Cryptography, edited by Bernstein, Buchmann and Dahmen. (A dead-tree copy of the book will run you $90, but you can check out Dan Berstein’s fantastic intro right here.)
Quantum vs. Classical
 |
| Quantum computers are only human. (Well, technically, they’re complicated machines full of super-cooled liquid nitrogen and helium.) |
There are many ways to build a classical computer. Whether you use transistors, gears, or photons, one thing binds all of these designs together: at any given moment, a classical computer should be in exactly one state.
To bring this back to cryptography, let’s say you’re trying to brute-force your way through the keyspace of a cryptosystem. In a classical computer this means trying one key at a time, for as many keys as it takes to get a useful result. Parallelization can speed this up, but ultimately just moves the problem sideways — trading resources for time.
Quantum computers use an entirely different model of computing. The fundamental component of a quantum computer is a quantum bit (‘qubit’), a value that can be in two states (1 and 0) at the same time. By entangling n qubits, it’s possible to construct a computer that exists in a ‘superposition’ of 2^n states simultaneously. And this is when things get interesting.
And complicated. Entrangling qubits is one thing (and not necessarily an easy thing). The real trick is finding a way to do computation with a computer that’s in more than one state, and — even more importantly — to pull a single ‘right’ answer back into our classical world once the computation is done.
These words obscure a lot of detail; an entire field’s worth of detail. What matters for our purposes is that in some cases it seems like quantum algorithms can harness this power to accomplish things much faster than classical algorithms. When this happens, it makes certain problems much easier (i.e., less time-consuming) to solve. But not every problem.
Quantum computers are not magic!
The important thing to know is that quantum computers can’t do everything. They can’t see the future. They can’t even (we believe) solve NP-complete problems in polynomial time. In fact, the general belief among researchers is that the class BQP — roughly, things that quantum computers can do efficiently — does not include all of NP (though in fairness, nobody knows for sure).
 |
| Proposed hierarchy of complexity classes with a guess for where BQP may fit. (Wikipedia) |
More importantly, anything that a quantum computer can do can also be done by a classical computer, though possibly with an exponential slowdown. This means that QCs aren’t going to do anything against information-theoretically secure cryptosystems, like the One Time Pad. Those schemes don’t care how powerful the attacker’s computer is.
Given these facts, you might not all that impressed with quantum computers right now. You’d be wrong.
An algorithm for a computer that doesn’t exist
The reason we’re so freaked out about quantum computing

is because of the harmless-looking gentleman above. Dr. Peter Shor claims responsibility for one of the most amazing, yet ostensibly useless, theoretical accomplishments in the history of computing: he developed a polynomial-time algorithm for factoring large integers. The only problem is that nobody has a computer that can run it.
I can only imagine how he explains this to his neighbors.
Shor’s algorithm actually has two components: (1) a classical portion that converts the factoring problem into an order-finding problem. And (2) a quantum portion that solves the latter in polynomial time (with some reasonable error probability). Shor’s algorithm can also be used to solve the Discrete Logarithm Problem (DLP) in fields and (with tweaks) elliptic curve groups.
The problem? Almost every practical public-key cryptosystem in use today depends on the hardness of the above problems. That includes RSA and Diffie-Hellman (both used in TLS), Elgamal (used in PGP), DSA and ECDSA (used to sign X.509 certificates, among other things), and even the Rabin cryptosystem (used primarily by Bram Cohen).
These are important algorithms, used today not just to protect short-term data, but also to encrypt data that may be still be important several decades from now. If anyone manages to build a reasonable quantum computer in that time, some people are going to be pretty unhappy.
I should quickly mention that Shor’s algorithm is not the only quantum algorithm that cryptographers care about — it just happens to be the most interesting one. There’s also Grover’s algorithm, which can be used to improve brute-force attacks on symmetric encryption schemes like AES. But the speedup from Grover’s algorithm is ‘only’ quadratic (it essentially halves the key length), not exponential like Shor’s algorithm. We can live with quadratic.
So what can we do about it?
With all the background out of the way, we can finally get to the point of this post. What can cryptographers do to deal with the looming potential of quantum computers? And when should we start doing it? There are a few answers to this question.
Solution #1: Business as usual
This is probably my favorite solution. Don’t do anything. Quantum computing is a long way off, and it may never happen at all. Let’s just keep doing what we’re doing, until we’re old enough that someone gives us a pension and we can dump the problem in someone else’s lap. Besides, isn’t there an asteroid heading towards the Earth?
No, this isn’t really a solution at all, but it seems to be the default mentality right now. It probably isn’t hurting us — for the moment.
Solution #2: Don’t overreact
While Shor’s algorithm is a pretty serious threat to RSA, (EC)DSA and most of the public-key algorithms we use in practice, these aren’t the only algorithms that we use. And the good news is that quantum computers probably won’t have the same effect on those.
AES, for example, would be affected by Grover’s algorithm, but only (in the absolute absurdly worst case), by reducing the effective key size by half. So a 256-bit key would still provide at least the same security margin as today’s 128-bit keys. We can probably live with that — and if not, we can always get bigger keys.
The only hole in this argument is that we have absolutely no idea what specific attacks people will develop against ciphers like AES in the future . Even now — using only classical algorithms — researchers have managed to shave a couple of bits off of the AES security margin. Quantum computers may substantially expand our toolbox.
Solution #3: Lattices, lattices, lattices!
 |
| (source/cc) |
If you haven’t been to a crypto conference lately, you haven’t been exposed to the new hotness in our field: lattice-based cryptography. Lattices are a mathematical structure that happens to turn up a lot in nature: for example, in the ordering of atoms in a crystal.
In a more abstract setting, lattice ‘problems’ — can be used to build a wide variety of cryptosystems. The best known examples include the NTRU scheme (used for encryption and signature) and Craig Gentry’s fully-homomorphic encryption scheme. But there are plenty more.
Lattices get a lot of attention these days, in part because you can do neat things with them (fully-homomorphic encryption is a great example). But a more general argument for lattice-based crypto is its resistance to quantum attacks. In contrast to factoring and DLP, there are no quantum algorithms known to run (substantially) faster than classical algorithms against the lattice problems we use to construct modern cryptosystems.
As with all of these claims, the keyword is ‘known’. Will we someday find such algorithms? Who knows. But deploying schemes that aren’t quantum-broken (yet) certainly feels a lot better than deploying schemes that are.
Solution #4: Fight fire with fire
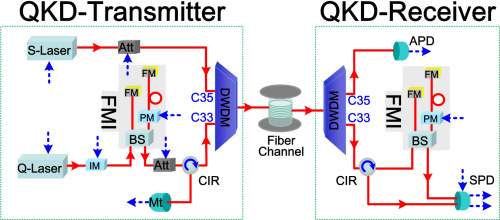 |
| QKD rig. (image source) |
The last, and possibly most desperate solution of all, is to dispense with computational problems altogether, and simply use the strength of quantum mechanics against itself.
This type of cryptography is known Quantum Key Distribution. QKD uses quantum-mechanical effects, rather than hard computational problems, to protect messages transmitted over a long distance.
The basic idea is quite simple: anyone who measures the quantum state of a particle must by definition change it (physics students: you’re welcome to correct me here!). The exception is entangled particles, which will both measure identically, even if the measurement is conducted at distant points. QKD rigs entangle particles, then transmit one set to a remote party via a long fiber-optic cable. If an attacker taps the cable and measures the particle, his tampering will be detected. If not, both parties can derive a random one-time pad, which they can then use to communicate. Quantum computers can’t do anything about this.
Unfortunately the more ‘perfect’ something sounds, the less you should trust it, especially if it’s a research system. This is what QKD researchers discovered last summer, when a team showed how to override the photon detectors in a QKD system with adversarially-generated signals of their own. The result: they were able to completely intercept the key without detection. This can all be fixed, but it goes to show that this is a harder problem than it looks.
More to the point, QKD requires a massive change in the way we distribute data. Today we send our ciphertexts through packet-switched networks, but QKD systems require dedicated fiber-optic connections between each participant. Thus, QKD isn’t likely to give us a good replacement for TLS anytime soon.
In summary
This has been yet another long post. Before I wrap up I just want to preemptively apologize to all of the physicists and quantum complexity theorists whose work I’ve mangled along the way.
No matter how terribly I’ve done this, the basic story is sound: quantum computers are at least theoretically possible, they’re quite likely to be practical, and they really will change a lot of things when they arrive. Mostly for the better. But not for the cryptosystems we use today.
If we don’t find a way to do something about this, the next few decades are going to be a very interesting time for crypto. For this reason alone, I’m hoping that asteroid isn’t coming; I’d really like to see how it all turns out.
Hey very good post! I'd be curious how you expect quantum cryptography to impact security protocols. For example AES might be secure, but if Diffie–Hellman is broken have fun exchanging your session keys ;p Also I'd just like to state that my opinion is that QKD is a horrible idea with great marketing. It still requires the use of traditional crypto, (it just does key exchange and requires a signaling channel authenticated with traditional crypto), is open to all sorts of side channel attacks with a horrible failure mode, and is so expensive that it'd be cheaper to hire a trusted courier to go to the remote site and drop off a stack of BlueRay disks filled with key material instead.
Hi there, good post. Some of your info on QKD is a little inaccurate though.
e.g. While currently implemented quantum networks require point-to-point links or trusted nodes in between, that won't be true in the future. If two parties share entangled particles then they can communicate via QKD. In a quantum repeater network entanglement can be distributed to any two parties desired with no dedicated point-to-point link required between them via chained entanglement swapping. The sender and receiver do not need to trust the network either, since the statistics of their own measurements will allow them to bound the information anyone else could possibly have.
The real current limitation for quantum networks is distance. Dedicated links become over fiber and in the atmosphere become too lossy to perform QKD over after just a few hundred kilometers (unless you use an orbital mirror, which could stretch this by quite a bit since there is no loss in vacuum). All current QKD networks are hobbled by this. Fortunately, if you add quantum memory (with greater than 50% efficiency) to quantum repeaters you can solve the distance problem.
Quantum memory is currently cutting edge research. A handful of groups in the world have made single-photon storage work, but usually with draw-backs that make them impractical for use in real world quantum repeater networks at present. However, this field is moving *fast*. Once quantum memory matures we should start seeing real-world quantum repeater networks that will allow network topologies quite similar to classical networks. They may even be able to use currently installed fiber optic links!
There are still significant problems to overcome though. Public key encryption is actually phenomenally nice in that it provides not just encryption, but authentication as well. Authentication in quantum networks is currently problematic. If any cryptographers out there really want to break into the QKD field in a big way, come up with a quantum authentication protocol!
Hey, thanks for the reply! I've spent a lot of time thinking about how to respond, since I'll freely admit I'm not an expert on the physics behind QKD. Luckily when talking about the security weaknesses I can focus on things like the protocols QKD uses and assume the physics side works as intended ;p
You certainly addressed the cost issue, and I agree with you that as time goes on, costs will certainly decrease. In retrospect I shouldn't have been snarky and listed that as one of my big objections.
I will stick by my security concerns of currently proposed QKD schemes though. First off, current systems have been shown to be highly vulnerable to side channel attacks, (such as the attacker determining the state of the filter or blinding the sensors). Like costs, this is an “engineering problem” so these vulnerabilities certainly could be addressed eventually, but the fact that QKD adds a whole slew of potential side-channel attacks is worth mentioning.
In addition, QKD is dependent on “traditional” crypto algorithms, both for encryption using the exchanged keys and for exchanging info on the control channel about which bits to use. More importantly, the addition of a control channel and the fact that an attacker can still read/modify a certain percentage of bits on the quantum channel without being detected opens up all sorts of interesting attacks. For example, I've seen one-time pads mentioned frequently as an encryption algorithm to use with keys distributed via QKD, (check out the QKD wiki article … admittedly not the most robust source but hey this is an example ;). If an attacker can control a couple of bits in the key though … well one time pads are generally a bad idea.
I could keep on talking about potential attacks but I guess my real problem with QKD is the marketing behind it. When I see companies like MagicQ making statements such as “quantum encryption can never be broken”, that really worries me since it's not true.
http://magiqtech.com/MagiQ/Products_files/8505_Data_Sheet.pdf
Lattices are great, but for post-quantum digital signatures, I think hash-based are better.
The argument is that if you had a lattice-based digital signature algorithm, you'd need a collision-resistant hash to generate message representatives from messages and then you'd use the lattice-based digital signature on the message representative. Therefore, the scheme would be vulnerable to a break in the lattice-based digital signature or in the collision-resistant hash function.
On the other hand, if you used a hash-based digital signature, then the scheme would be vulnerable only the a break in the hash function. That's better!
(This argument is due to David-Sarah Hopwood.)
Great article, I'll definitely share this for sure. Thank you very much.
Nice article …
I agree that if quantum repeater can be built successfully, it gonna support QKD network and many QKD protocols can be deployed. But still, it requires special infrastructure, i.e point-to-point all-optical network.
Imagine, our mobile phone has free space quantum detector? We could store some pre-entangled photon in our internal quantum memory? Probably these group of photons are our private key ….
I truly appreciate simply examining your entire websites. Basically desired to let you know which you have folk just like me who appreciate your work. Absolutely a great post. Hats off to you! The information which you have provided is very helpful.
You've got so much to state much to give. I really hope folks realize this look at into your page.
I am truly satisfied I spent the time to learn on over the very first section.
This article gives the light in which we can observe the reality. This is very nice one and gives in-depth information. Thanks for this nice article.
agen bola
Thanks for the amazing content on your blog I am very interested in this article and you have really helped me. I have just told a few of my friends about this on FaceBook and they love your content just as much as I do.
Jasa SEO