Category: TLS/SSL

Attack of the week: RC4 is kind of broken in TLS

Update: I’ve added a link to a page at Royal Holloway describing the new attack. 

Listen, if you’re using RC4 as your primary ciphersuite in SSL/TLS, now would be a great time to stop. Ok, thanks, are we all on the same page?

No?

I guess we need to talk about this a bit more. You see, these slides have been making the rounds since this morning. Unfortunately, they contain a long presentation aimed at cryptographers, and nobody much seems to understand the real result that’s buried around slide 306 (!). I’d like to help.

Here’s the short summary:

According to AlFardan, Bernstein, Paterson, Poettering and Schuldt (a team from Royal Holloway, Eindhoven and UIC) the RC4 ciphersuite used in SSL/TLS is broken. If you choose to use it — as do a ridiculous number of major sites, including Google — then it may be possible for a dedicated attacker to recover your authentication cookies. The current attack is just on the edge of feasibility, and could probably be improved for specific applications.

This is bad and needs to change soon.

In the rest of this post I’ll cover the details in the usual ‘fun’ question-and-answer format I save for these kinds of attacks.

What is RC4 and why should I care?

RC4 is a fast stream cipher invented in 1987 by Ron Rivest. If you like details, you can see this old post of mine for a longwinded discussion of RC4’s history and flaws. Or you can take my word: RC4 is old and crummy.

Despite its age and crumminess, RC4 has become an extremely popular ciphersuite for SSL/TLS connections — to the point where it accounts for something absurd like half of all TLS traffic. There are essentially two reasons for this:

  1. RC4 does not require padding or IVs, which means it’s immune to recent TLS attacks like BEAST and Lucky13. Many admins have recommended it as the solution to these threats.
  2. RC4 is pretty fast. Faster encryption means less computation and therefore lower hardware requirements for big service providers like Google.

So what’s wrong with RC4?

Like all stream ciphers, RC4 takes a short (e.g., 128-bit) key and stretches it into a long string of pseudo-random bytes. These bytes are XORed with the message you want to encrypt, resulting in what should be a pretty opaque (and random-looking) ciphertext.

The problem with RC4 is that the above statement is not quite true. The bytes come out of the RC4 aren’t quite random looking — they have small biases. A few of these biases have been known for years, but weren’t considered useful. However, recent academic work has uncovered many small but significant additional biases running throughout the first 256 bytes of RC4 output. This new work has systematically identified many more.

At first blush this doesn’t seem like a big deal. Cryptographically, however, it’s a disaster. If I encrypt the same message (plaintext) with many different RC4 keys, then I should get a bunch of totally random looking ciphertexts. But these tiny biases mean that they won’t be random — a statistical analysis of different positions of the ciphertext will show that some values occur more often.

By getting many different encryptions of the same message — under different keys — I can tally up these small deviations from random and thus figure out what was encrypted.

If you like analogies, think of it like peeking at a picture with your hands over your eyes. By peeking through your fingers you might only see a tiny sliver of the scene you’re looking at. But by repeating the observation many times, you may be able to combining those slivers and figure out what you’re looking at.

Why would someone encrypt the same message many times?

The problem here (as usual) is your browser.

You see, there are certain common elements that your browser tends to send at the beginning of every HTTP(S) connection. One of these values is a cookie — typically a fixed string that identifies you to a website. These cookies are what let you log into Gmail without typing your password every time.

If you use HTTPS (which is enforced in many sites by default), then your cookies should be safe. After all, they’ll always be sent over an encrypted connection to the website.Unfortunately, if your connection is encrypted using RC4 (as is the case with Gmail), then each time you make a fresh connection to the Gmail site, you’re sending a new encrypted copy of the same cookie. If the session is renegotiated (i.e., uses a different key) between those connections, then the attacker can build up the list of ciphertexts he needs.

To make this happen quickly, an attacker can send you a piece of Javascript that your browser will run — possibly on a non-HTTPS tab. This Javascript can then send many HTTPS requests to Google, ensuring that an eavesdropper will quickly build up thousands (or millions) of requests to analyze.

Probability of recovering a plaintext byte (y axis) at a particular byte position in the RC4-encrypted stream (x axis), assuming 2^24 ciphertexts. Increasing the number of ciphertexts to 2^32 gives almost guaranteed plaintext recovery at all positions. (source)

Millions of ciphertexts? Pah. This is just crypto-wankery.

It’s true that the current attack requires an enormous number of TLS connections — in the tens to hundreds of millions — which means that it’s not likely to bother you. Today. On the other hand, this is the naive version of the attack, without any special optimizations.

For example, the results given by Bernstein assume no prior plaintext knowledge. But in practice we often know a lot about the structure of an interesting plaintext like a session cookie. For one thing, they’re typically Base64 encoded — reducing the number of possibilities for each byte — and they may have some recognizable structure which can be teased out using advanced techniques.

It’s not clear what impact these specific optimizations will have, but it tends to reinforce the old maxim: attacks only get better, they never get worse. And they can get a lot better while you’re arguing about them.

So what do we do about it?

Treat this as a wakeup call. Sites (like Google) need to stop using RC4 — before these attacks become practical. History tells us that nation-state attackers are already motivated to penetrate Gmail connections. The longer we stick with RC4, the more chances we’re giving them.

In the short term we have an ugly choice: stick with RC4 and hope for the best, or move back to CBC mode ciphersuites — which many sites have avoided due to the BEAST and Lucky13 attacks.

We could probably cover ourselves a bit by changing the operation of browsers, so as to detect and block Javascript that seems clearly designed to exercise these attacks. We could also put tighter limits on the duration and lifespan of session cookies. In theory we could also drop the first few hundred bytes of each RC4 connection — something that’s a bit of a hack, and difficult to do without breaking the TLS spec.

In the longer term, we need to move towards authenticated encryption modes like the new AEAD TLS ciphersuites, which should put an end to most of these problems. The problem is that we’ll need browsers to support these modes too, and that could take ages.

In summary

I once made fun of Threatpost for sounding alarmist about SSL/TLS. After all, it’s not like we really have an alternative. But the truth is that TLS (in its design, deployment and implementation) needs some active help. We’re seeing too many attacks, and they’re far too close to practical. Something needs to give.

We live in a world where NIST is happy to give us a new hash function every few years. Maybe it’s time we put this level of effort and funding into the protocols that use these primitives? They certainly seem to need it.

Attack of the week: TLS timing oracles

Ever since I started writing this blog (and specifically, the posts on SSL/TLS) I’ve had a new experience: people come up to me and share clever attacks that they haven’t made public yet.

This is pretty neat — like being invited to join an exclusive club. Unfortunately, being in this club mostly sucks. That’s because the first rule of ‘TLS vulnerability club’ is: You don’t talk about TLS vulnerability club. Which takes all the fun out of it.

(Note that this is all for boring reasons — stuff like responsible disclosure, publication and fact checking. Nobody is planning a revolution.)

Anyway, it’s a huge relief that I’m finally free to tell you about a neat new TLS attack I learned about recently. The new result comes from Nadhem AlFardan and Kenny Paterson of Royal Holloway. Dubbed ‘Lucky 13’, it takes advantage of a very subtle bug in the way records are encrypted in the TLS protocol.

If you aren’t into long crypto posts, here’s the TL;DR:

There is a subtle timing bug in the way that TLS data decryption works when using the (standard) CBC mode ciphersuite. Given the right set of circumstances, an attacker can use this to completely decrypt sensitive information, such as passwords and cookies. 

The attack is borderline practical if you’re using the Datagram version of TLS (DTLS). It’s more on the theoretical side if you’re using standard TLS. However, with some clever engineering, that could change in the future. You should probably patch!

For the details, read on. As always, we’ll do this in the ‘fun’ question/answer format I save for these kinds of posts.

What is TLS, what is CBC mode, and why should I care if it’s broken?

Some background: Transport Layer Security (née SSL) is the most important security protocol on the Internet. If you find yourself making a secure connection to another computer, there’s a very good chance you’ll be doing it with TLS. (Unless you’re using UDP-based protocol, in which case you might use TLS’s younger cousin Datagram TLS [DTLS]).

The problem with TLS is that it kind of stinks. Mostly this is due to bad decisions made back in the the mid-1990s when SSL was first designed. Have you seen the way people dressed back then? Protocol design was worse.

While TLS has gotten better since then, it still retains many of the worst ideas from the era. One example is the CBC-mode ciphersuite, which I’ve written about several times before on this blog. CBC-mode uses a block cipher (typically AES) to encrypt data. It’s the most common ciphersuite in use today, probably because it’s the only mandatory ciphersuite given in the spec.

What’s wrong with CBC mode?

The real problem with TLS is not the encryption itself, but rather the Message Authentication Code (MAC) that’s used to protect the integrity (authenticity) of each data record.

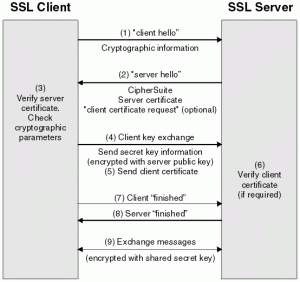
Our modern understanding is that you should always encrypt a message first, then apply the MAC to the resulting ciphertext. But TLS gets this backwards. Upon encrypting a record, the sender first applies a MAC to the plaintext, then adds up to 255 bytes of padding to get the message up to a multiple of the cipher (e.g., AES’s) block size. Only then does it CBC-encrypt the record.

Structure of a TLS record. The whole thing is encrypted with CBC mode.

The critical point is that the padding is not protected by the MAC. This means an attacker can tamper with it (by flipping specific bits in the ciphertext), leading to a very nasty kind of problem known as a padding oracle attack.

In these attacks (example here), an attacker first captures an encrypted record sent by an honest party, modifies it, then re-transmits it to the server for decryption. If the attacker can learn whether her changes affected the padding — e.g., by receiving a padding error as opposed to a bad MAC error — she can use this information to adaptively decrypt the whole record. The structure of TLS’s encryption padding makes it friendly to these attacks.

Closeup of a padded TLS record. Each byte contains the padding length, followed by another (pointless, redundant) length byte.

But padding oracle attacks are well known, and (D)TLS has countermeasures!

The TLS designers learned about padding oracles way back in 2002, and immediately took steps to rectify them. Unfortunately, instead of fixing the problem, they decided to apply band-aids. This is a time-honored tradition in TLS design.

The first band-aid was simple: eliminate any error messages that could indicate to the attacker whether the padding check (vs. the MAC check) is what caused a decryption failure.

This seemed to fix things for a while, until some researchers figured out that you could simply time the server to see how long decryption takes, and thereby learn if the padding check failed. This is because implementations of the time would first check the padding, then return immediately (without checking the MAC) if the padding was bad. That resulted in a noticeable timing differential the attacker could detect.

Thus a second band-aid was needed. The TLS designers decreed that decryption should always take the same amount of time, regardless of how the padding check comes out. Let’s roll the TLS 1.2 spec:

[T]he best way to do this is to compute the MAC even if the padding is incorrect, and only then reject the packet. For instance, if the pad appears to be incorrect, the implementation might assume a zero-length pad and then compute the MAC.

Yuck. Does this even work?

Unfortunately, not quite. When the padding check fails, the decryptor doesn’t know how much padding to strip off. That means they don’t know how long the actual message is, and therefore how much data to MAC. The recommended countermeasure (above) is to assume no padding, then MAC the whole blob. As a result, the MAC computation can take a tiny bit longer when the padding is damaged.

The TLS designers realized this, but by this point they were exhausted and wanted to go think about something else. So they left us with the following note:

This leaves a small timing channel, since MAC performance depends to some extent on the size of the data fragment, but it is not believed to be large enough to be exploitable, due to the large block size of existing MACs and the small size of the timing signal.

And for the last several years — at least, as far as we know — they were basically correct.

How does this new paper change things?

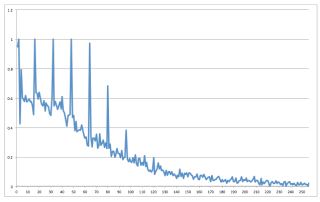
The new AlFardan and Paterson result shows that it is indeed possible to distinguish the tiny timing differential caused by invalid padding, at least from a relatively close distance — e.g., over a LAN. This is partly due to advances in computing hardware: most new computers now ship with an easily accessible CPU cycle counter. But it’s also thanks to some clever statistical techniques that use many samples to smooth out and overcome the jitter and noise of a network connection.

The upshot is that new technique can measure timing differentials of less than 1 microsecond over a LAN connection — for example, if the attacker is in the same data center as your servers. It does this by making several thousand decryption queries and processing the results. Under the right circumstances, this turns out to be enough to bring (D)TLS padding oracle attacks back to life.

How does the attack work?

For the details, you should obviously read the full paper or at least the nice FAQ that Royal Holloway has put out. Here I’ll try to give some intuition.

Before I can explain the attack, you need to know a little bit about how hash-based MACs work. TLS typically uses HMAC with either MD5, SHA1 or SHA256 as the hash function. While these are very different hash functions, the critical point is that each one processes messages in 64-byte blocks.

Consequently, hashing time is a function of the number of blocks in the message, not the number of bytes. Going from a 64-byte input to a 65-byte input means an entire extra block, and hence a (relatively) large jump in the amount of computation time (an extra iteration of the hash function’s compression function).

There are a few subtleties in here. The hash functions incorporate an 8-byte length field plus some special hash function padding, which actually means a one-block message can only contain about 55 bytes of real data (which also includes the 13-byte record header). The HMAC construction adds a (constant) amount of additional work, but we don’t need to think about that here.

So in summary: you can get 55 bytes of data into one block of the hash. Go a single byte beyond that, and the hash function will have to run a whole extra round, causing a tiny (500-1000 hardware cycle) delay.

The attack here is to take a message that — including the TLS padding — would fall above that 55 byte boundary. However, the same message with padding properly removed would fall below it. When an attacker tampers with the message (damaging the padding), the decryption process will MAC the longer version of the message — resulting in a measurably higher computation time than when the padding checks out.

By repeating this process many, many thousand (or millions!) of times to eliminate noise and network jitter, it’s possible to get a clear measurement of whether the decryption succeeded or not. Once you get that, it’s just a matter of executing a standard padding oracle attack.

But there’s no way this will work on TLS! It’ll kill the session!

Please recall that I described this as a practical attack on Datagram TLS (DTLS) — and as a more theoretical one on TLS itself.* There’s a reason for this.

The reason is that TLS (and not DTLS) includes one more countermeasure I haven’t mentioned yet: anytime a record fails to decrypt (due to a bad MAC or padding error), the TLS server kills the session. DTLS does not do this, which makes this attack borderline practical. (Though it still takes millions of packet queries to execute.)

The standard TLS ‘session kill’ feature would appear to stop padding oracle attacks, since they require the attacker to make many, many decryption attempts. Killing the session limits the attacker to one decryption — and intuitively that would seem to be the end of it.

But actually, this turns out not to be true.

You see, one of the neat things about padding oracle attacks is that they can work across different sessions (keys), provided that that (a) your victim is willing to re-initiate the session after it drops, and (b) the secret plaintext appears in the same position in each stream. Fortunately the design of browsers and HTTPS lets us satisfy both of these requirements.

  1. To make a target browser initiate many connections, you can feed it some custom Javascript that causes it to repeatedly connect to an SSL server (as in the CRIME attack). Note that the Javascript doesn’t need to come from the target webserver — it can even served on an unrelated non-HTTPS page, possibly running in a different tab. So in short: this is pretty feasible.
  2. Morover, thanks to the design of the HTTP(S) protocol, each of these connections will include cookies at a known location in HTTP stream. While you may not be able to decrypt the rest of the stream, these cookie values are generally all you need to break into somebody’s account.

Thus the only practical limitation on such a cookie attack is the time it takes for the server to re-initiate all of these connections. TLS handshakes aren’t fast, and this attack can take tens of thousands (or millions!) of connections per byte. So in practice the TLS attack would probably take days. In other words: don’t panic.

On the other hand, don’t get complacent either. The authors propose some clever optimizations that could take the TLS attack into the realm of the feasible (for TLS) in the near future.

How is it being fixed?

With more band-aids of course!

But at least this time, they’re excellent band-aids. Adam Langley has written a 500-line OpenSSL patch (!) that modifies the CBC-mode decryption procedure to wipe out the timing differentials used by this attack. I would recommend that you think about updating at least your servers in the future (though we all know you won’t). Microsoft products should also see updates soon are allegedly not vulnerable to this attack, so won’t need updates.**

Still, this is sort of like fixing your fruitfly problem by spraying your kitchen with DDT. Why not just throw away the rotted fruit? In practice, that means moving towards modern AEAD ciphersuites like AES-GCM, which should generally end this madness. We hope.

Why not switch to RC4?

RC4 is not an option in DTLS. However, it will mitigate this issue for TLS, since the RC4 ciphersuite doesn’t use padding at all. In fact, this ancient ciphersuite has been (hilariously) enjoying a resurgence in recent years as the ‘solution’ to TLS attacks like BEAST. Some will see this attack as further justification for the move.

But please don’t do this. RC4 is old and creaky, and we really should be moving away from it too.

So what’s next for TLS?

I’d love to say more, but you see, the first rule of TLS vulnerability club is…

Notes:

* The attack on Datagram TLS is more subtle, and a lot more interesting. I haven’t covered it much in this post because TLS is much more widely used than DTLS. But briefly, it’s an extension of some previous techniques — by the same authors — that I covered in this blog last year. The gist is that an attacker can amplify the impact of the timing differential by ‘clogging’ the server with lots of unrelated traffic. That makes these tiny differentials much easier to detect.

** And if you believe that, I have a lovely old house in Baltimore to sell you…

Surveillance works! Let’s have more of it.

If you care about these things, you might have heard that Google recently detected and revoked a bogus Google certificate. Good work, and huge kudos to the folks at Google who lost their holidays to this nonsense.

From what I’ve read, this particular incident got started in late 2011 when Turkish Certificate Authority TURKTRUST accidentally handed out intermediate CA certificates to two of their customers. Intermediate CA certs are like normal SSL certs, with one tiny difference: they can be used to generate other SSL certificates. Oops.

One of the recipients noticed the error and reported it to the CA. The other customer took a different approach and installed it into an intercepting Checkpoint firewall to sniff SSL-secured connections. Because, you know, why not.

So this is bad but not exactly surprising — in fact, it’s all stuff we’ve seen before. Our CA system has far too many trust points, and it requires too many people to act collectively when someone proves untrustworthy. Unless we do something, we’re going to see lots more of this.

What’s interesting about this case — and what leads to the title above — is not so much what went wrong, but rather, what went right. You see, this bogus certificate was detected, and likely not because some good samaritan reported the violation. Rather, it was (probably) detected by Google’s unwavering surveillance.

The surveillance in question is conducted by the Chrome brower, which actively looks out for attacks and reports them. Here’s the money quote from their privacy policy:

“If you attempt to connect to a Google website using a secure
connection, and the browser blocks the connection due to information
that indicates you are being actively attacked by someone on the
network (a “man in the middle attack”), Chrome may send information
about that connection to Google for the purpose of helping to
determine the extent of the attack and how the attack functions.”

The specific technical mechanism in Chrome simple: Chrome ships with a series of ‘pins’ in its source code (thanks Moxie, thanks Tom). These tell Chrome what valid Google certificates should look like, and help it detect an obviously bogus certificate. When Chrome sees a bogus cert attached to a purported Google site, it doesn’t just stop the connection, it rings an alarm at Google HQ.

And that alarm is a fantastic thing, because in this case it may have led to discovery and revocation before this certificate could be stolen and used for something worse.

Now imagine the same thing happening in many other browsers, and not just for Google sites. Well, you don’t have to imagine. This is exactly the approach taken by plugins like Perspectives and Convergence, which monitor users’ SSL connections in a distributed fashion to detect bogus certificates. These plugins are great, but they’re not deployed widely enough. The technique should be standard in all browsers, perhaps with some kind of opt in. (I certainly would opt.)

The simple fact is that our CA system is broken and this is what we’ve got. Congratulations to Google for taking a major first step in protecting its users. Now let’s take some more.

On the (provable) security of TLS: Part 2

This is the second post in a series on the provable security of TLS. If you haven’t read the first part, you really should!

The goal of this series is to try to answer an age-old question that is often asked and rarely answered. Namely: is the TLS protocol provably secure?

While I find the question interesting in its own right, I hope to convince you that it’s of more than academic interest. TLS is one of the fundamental security protocols on the Internet, and if it breaks lots of other things will too. Worse, it has broken — repeatedly. Rather than simply patch and hope for the best, it would be fantastic if we could actually prove that the current specification is the right one.

Unfortunately this is easier said than done. In the first part of this series I gave an overview of the issues that crop up when you try to prove TLS secure. They come at you from all different directions, but most stem from TLS’s use of ancient, archaic cryptography; gems like, for example, the ongoing use of RSA-PKCS#1v1.5 encryption fourteen years after it was shown to be insecure.

Despite these challenges, cryptographers have managed to come up with a handful of nice security results on portions of the protocol. In the previous post I discussed Jonnson and Kaliski’s proof of security for the RSA-based TLS handshake. This is an important and confidence-inspiring result, given that the RSA handshake is used in almost all TLS connections.

In this post we’re going to focus on a similarly reassuring finding related to the the TLS record encryption protocol — and the ‘mandatory’ ciphersuites used by the record protocol in TLS 1.1 and 1.2 (nb: TLS 1.0 is broken beyond redemption). What this proof tells us is that TLS’s CBC mode ciphersuites are secure, assuming… well, a whole bunch of things, really.

The bad news is that the result is extremely fragile, and owes its existence more to a series of happy accidents than from any careful security design. In other words, it’s just like TLS itself.

Records and handshakes

Let’s warm up with a quick refresher.

TLS is a layered protocol, with different components that each do a different job. In the previous post I mostly focused on the handshake, which is a beefed-up authenticated key agreement protocol. Although the handshake does several things, its main purpose is to negotiate a shared encryption key between a client and a server — parties who up until this point may be complete strangers.

The handshake gets lots of attention from cryptographers because it’s exciting. Public key crypto! Certificates! But really, this portion of the protocol only lasts for a moment. Once it’s done, control heads over to the unglamorous record encryption layer which handles the real business of the protocol: securing application data.

Most kids don’t grow up dreaming about a chance to work on the TLS record encryption layer, and that’s fine — they shouldn’t have to. All the record encryption layer does is, well, encrypt stuff. In 2012 that should be about as exciting as mailing a package.

And yet TLS record encryption still manages to be a source of endless excitement! In the past year alone we’ve seen three critical (and exploitable!) vulnerabilities in this part of TLS. Clearly, before we can even talk about the security of record encryption, we have to figure out what’s wrong with it.

Welcome to 1995

Development of the SSLv1
record encryption layer

The problem (again) is TLS’s penchant for using prehistoric cryptography, usually justified on some pretty shaky ‘backwards compatibility‘ grounds. This excuse is somewhat bogus, since the designers have actually changed the algorithms in ways that break compatibility with previous versions — and yet retained many of the worst features of the originals.

The most widely-used ciphersuites employ a block cipher configured in CBC mode, along with a MAC to ensure record authenticity. This mode can be used with various ciphers/MAC algorithms, but encryption always involves the following steps:

  1. If both sides support TLS compression, first compress the plaintext.
  2. Next compute a MAC over the plaintext, record type, sequence number and record length. Tack the MAC onto the end of the plaintext.
  3. Pad the result with up to 256 bytes of padding, such that the padded length is a multiple of the cipher’s block size. The last byte of the padding should contain the padding length (excluding this byte), and all padding bytes must also contain the same value. A padded example (with AES) might look like:

    0x MM MM MM MM MM MM MM MM MM 06 06 06 06 06 06 06

  4. Encrypt the padded message using CBC mode. In TLS 1.0 the last block of the previous ciphertext (called the ‘residue’) is used as the Initialization Vector. Both TLS 1.1 and 1.2 generate a fresh random IV for each record.
Upon decryption the attacker verifies that the padding is correctly structured, checks the MAC, and outputs an error if either condition fails.

To get an idea of what’s wrong with the CBC ciphersuite, you can start by looking at the appropriate section of the TLS 1.2 spec — which reads more like the warning label on a bottle of nitroglycerin than a cryptographic spec. Allow me sum up the problems.

First, there’s the compression. It’s long been known that compression can leak information about the contents of a plaintext, simply by allowing the adversary to see how well it compresses. The CRIME attack recently showed how nasty this can get, but the problem is not really news. Any analysis of TLS encryption begins with the assumption that compression is turned off.

Next there’s the issue of the Initialization Vectors. TLS 1.0 uses the last block of the previous ciphertext, which is absurd, insecure and — worse — actively exploitable by the BEAST attack. Once again, the issue has been known for years yet was mostly ignored until it was exploited.

So ok: no TLS 1.0, no compression. Is that all?

Well, we still haven’t discussed the TLS MAC, which turns out to be in the wrong place — it’s applied before the message is padded and encrypted. This placement can make the protocol vulnerable to padding oracle attacks, which (amazingly) will even work across handshakes. This last fact is significant, since TLS will abort the connection (and initiate a new handshake) whenever a decryption error occurs in the record layer. It turns out that this countermeasure is not sufficient.

To deal with this, recent versions of TLS have added the following patch: they require implementers to hide the cause of each decryption failure — i.e., make MAC errors indistinguishable from padding failures. And this isn’t just a question of changing your error codes, since clever attackers can learn this information by measuring the time it takes to receive an error. From the TLS 1.2 spec:

In general, the best way to do this is to compute the MAC even if the padding is incorrect, and only then reject the packet. For instance, if the pad appears to be incorrect, the implementation might assume a zero-length pad and then compute the MAC. This leaves a small timing channel, since MAC performance depends to some extent on the size of the data fragment, but it is not believed to be large enough to be exploitable.

To sum up: TLS is insecure if your implementation leaks the cause of a decryption error, but careful implementations can avoid leaking much, although admittedly they probably will leak some — but hopefully not enough to be exploited. Gagh!

At this point, just take a deep breath and say ‘all horses are spherical‘ three times fast, cause that’s the only way we’re going to get through this.

Accentuating the positive

Having been through the negatives, we’re almost ready to say nice things about TLS. Before we do, let’s just take a second to catch our breath and restate some of our basic assumptions:

  1. We’re not using TLS 1.0 because it’s broken.
  2. We’re not using compression because it’s broken.
  3. Our TLS implementation is perfect — i.e., doesn’t leak any information about why a decryption failed. This is probably bogus, yet we’ve decided to look the other way.
  4. Oh yeah: we’re using a secure block cipher and MAC (in the PRP and PRF sense respectively).**

And now we can say nice things. In fact, thanks to a recent paper by Kenny Paterson, Thomas Ristenpart and Thomas Shrimpton, we can say a few surprisingly positive things about TLS record encryption.

What Paterson/Ristenpart/Shrimpton show is that TLS record encryption satisfies a notion they call ‘length-hiding authenticated encryption‘, or LHAE. This new (and admittedly made up) notion not only guarantees the confidentiality and authenticity of records, but ensures that the attacker can’t tell how long they are. The last point seems a bit extraneous, but it’s important in the case of certain TLS libraries like GnuTLS, which actually add random amounts of padding to messages in order to disguise their length.

There’s one caveat to this proof: it only works in cases where the MAC has an output size that’s greater or equal to the cipher’s block size. This is, needless to say, a totally bizarre and fragile condition for the security of a major protocol to hang on. And while the condition does hold for all of the real TLS ciphersuites we use — yay! — this is more a happy accident than the result of careful design on anyone’s part. It could easily have gone the other way.

So how does the proof work?

Good question. Obviously the best way to understand the proof is to read the paper itself. But I’d like to try to give an intuition.

First of all, we can save a lot of time by starting with the fact that CBC-mode encryption is already known to be IND-CPA secure if implemented with a secure block cipher (PRP). This result tells us only that CBC is secure against passive attackers who can request the encryption of chosen messages. (In fact, a properly-formed CBC mode ciphertext should be indistinguishable from a string of random bits.)

The problem with plain CBC-mode is that these security results don’t hold in cases where the attacker can ask for the decryption of chosen ciphertexts.

This limitation is due to CBC’s malleability — specifically, the fact that an attacker can tamper with a ciphertext, then gain useful information by sending the result to be decrypted. To show that TLS record encryption is secure, what we really want to prove is that tampering gives no useful results. More concretely, we want to show that asking for the decryption of a tampered ciphertext will always produce an error.

We have a few things working in our favor. First, remember that the underlying TLS record has a MAC on it. If the MAC is (PRF) secure, then any ciphertext tampering that results in a change to this record data or its MAC will be immediately detected (and rejected) by the decryptor. This is good.

Unfortunately the TLS MAC doesn’t cover the padding. To continue our argument, we need to show that no attacker can produce a legitimate ciphertext, and that includes tampering that messes with the padding section of the message. Here again things look intuitively good for TLS. During decryption, the decryptor checks the last byte of the padded message to see how much padding there is, then verifies that all padding bytes contain the same numeric value. Any tampering that affects this section of the plaintext should either:

  1. Produce inconsistencies in some padding bytes, resulting in a padding error, or
  2. Cause the wrong amount of padding to be stripped off, resulting in a MAC error.
Both of these error conditions will appear the same to the attacker, thanks to the requirement that TLS implementations hide the reason for a decryption failure. Once again, the attacker should learn nothing useful.

This all seems perfectly intuitive, and you can imagine the TLS developers making exactly this argument as they wrote up the spec. However there’s one small exception to the rule above, which can turn TLS implementations that add an unnecessarily large amount of padding to the plaintext. (For example, GnuTLS.)

To give an example, let’s say the unpadded record + MAC is 15 bytes. If we’re using AES, then this plaintext can be padded with a single byte. Of course, if we’re inclined to add extra padding, it could also be padded with seventeen bytes — both are valid padding strings. The two possible paddings are presented below:

If the extra-long padding is used, the attacker could maul the longer ciphertext by truncating it — throwing away the last 16-byte ciphertext block. Truncation is a viable way to maul CBC ciphertexts, since it has the same effect on the underlying plaintext. The CBC decryption of the truncated ciphertext would yield:
Which not very useful, since the invalid padding would lead to a decryption error. However, the attacker could fix this — this time, using the fact that TLS can be mauled by flipping bits in the last byte of the Initialization Vector. Such an attack would allow the attacker to convert that trailing 0x10 into an 0x00. This result is now valid ciphertext that will not produce an error on decryption.
So what has the attacker learned by this attack? In practice, not very much. Mostly what they know is the length of the original ciphertext — so much for GnuTLS’s attempt to disguise the length. But more fundamentally: this attacker of ‘mauling’ the ciphertext totally screws up the nice idea we were going for in our proof.
So the question is: can this attack be used against real TLS? And this is where the funny restriction about MAC size comes into play.

You see, if TLS MACs are always bigger than a ciphertext block, then all messages will obey a strict rule: no padding will ever appear in the first block of the CBC ciphertext.

Since the padding is now guaranteed to start in the second (or later) block of the CBC ciphertext, the attacker cannot ‘tweak’ it by modifying the IV (this attack only works against the first block of the plaintext). Instead, they would have to tamper with a ciphertext block. And in CBC mode, tampering with ciphertext blocks has consequences! Such a tweak will allow the attacker to change padding bytes, but as a side effect it will cause one entire block of the record or MAC to be randomized when decrypted. And what Paterson/Ristenpart/Shrimpton prove is that this ‘damage’ will inevitably lead to a MAC error.

This ‘lucky break’ means that an attacker can’t successfully tamper with a CBC-mode TLS ciphertext. And that allows us to push our way to a true proof of the CBC-mode TLS ciphersuites. By contrast, if the MAC was only 80 bits (as it is in some IPSEC configurations), the proof would not be possible. So it goes.

Now I realize this has all been pretty wonky, and that’s kind of the point! The moral to the story is that we shouldn’t need this proof in the first place! What it illustrates is how fragile and messy the TLS design really is, and how (once again) it achieves security by luck and the skin of its teeth, rather than secure design.

What about stream ciphers?

The good news — to some extent — is that none of the above problems apply to stream ciphers, which don’t attempt to hide the record length, and don’t use padding in the first place. So the security of these modes is much ‘easier’ to argue.

Of course, this is only ‘good news’ if you believe that the stream ciphers included with TLS are good in the first place. The problem, of course, is that the major supported stream cipher is RC4. I will leave it to the reader to decide if that’s a worthwhile tradeoff.

In conclusion

There’s probably a lot more that can be said about TLS record encryption, but really… I think this post is probably more than anyone (outside of the academic community and a few TLS obsessives) has ever wanted to read on the subject.

In the next posts I’m going to come back to the much more exciting Diffie-Hellman handshake and then try to address the $1 million and $10 million questions respectively. First: does anyone really implement TLS securely? And second: when can we replace this thing?

Notes:

* One thing I don’t mention in this post is the TLS 1.0 ’empty fragment’ defense, which actually works against BEAST and has been deployed in OpenSSL for several years. The basic idea is to encrypt an empty record of length 0 before each record goes over the wire. In practice, this results in a full record structure with a MAC, and prevents attackers from exploiting the residue bug. Although nobody I know of has ever proven it secure, the proof is relatively simple and can be arrived at using standard techniques.

** The typical security definition for a MACs is SUF-CMA (strongly unforgeable under chosen message attack). This result uses the stronger — but also reasonable — assumption that the MAC is actually a PRF.

On the (provable) security of TLS: Part 1

If you sit a group of cryptographers down and ask them whether TLS is provably secure, you’re liable to get a whole variety of answers. Some will just giggle. Others will give a long explanation that hinges on the definitions of ‘prove‘ and ‘secure‘. What you will probably not get is a clear, straight answer.

In fairness, this is because there is no clear, straight answer. Unfortunately, like all the things you really need to know in life, it’s complicated.

Still, just because something’s complicated doesn’t mean that we get to ignore it. And the security of TLS is something we really shouldn’t ignore —  because TLS has quietly become the most important and trusted security protocol on the Internet. While plenty of security experts will point out the danger of improperly configured TLS setups, most tend to see (properly configured) TLS as a kind of gold standard — and it’s now used in all kinds of applications that its designers would probably never have envisioned.

And this is a problem, because (as Marsh points out) TLS (or rather, SSL) was originally designed to secure $50 credit card transactions, something it didn’t always do very well. Yes, it’s improved over the years. On the other hand, gradual improvement is no substitute for correct and provable security design.

All of which brings us to the subject of this — and subsequent — posts: even though TLS wasn’t designed to be a provably-secure protocol, what can we say about it today? More specifically, can we prove that the current version of TLS is cryptographically secure? Or is there something fundamental that’s holding it back?

The world’s briefest overview of TLS

If you’re brand new to TLS, this may not be the right post for you. Still, if you’re looking for a brief refresher, here it is:

TLS is a protocol for establishing secure (Transport layer) communications between two parties, usually denoted as a Client and a Server.

The protocol consists of several phases. The first is a negotiation, in which the two peers agree on which cryptographic capabilities they mutually support — and try to decide whether a connection is even possible. Next, the parties engage in a Key Establishment protocol that (if successful) authenticates one or both of the parties, typically using certificates, and allows the pair to establish a shared Master Secret. This is done using a handful of key agreement protocols, including various flavors of Diffie-Hellman key agreement and an RSA-based protocol.

Finally, the parties use this secret to derive encryption and/or authentication keys for secure communication. The rest of the protocol is very boring — all data gets encrypted and sent over the wire in a (preferably) secure and authenticated form. This image briefly sums it up:
sy10660a
Overview of TLS (source)

So why can’t we prove it secure?

TLS sounds very simple. However, it turns out that you run into a few serious problems when you try to assemble a security proof for the protocol. Probably the most serious holdup stems from the age of the cryptography used in TLS. To borrow a term from Eric Rescorla: TLS’s crypto is downright prehistoric.

This can mostly be blamed on TLS’s predecessor SSL, which was designed in the mid-90s — a period better known as ‘the dark ages of industrial crypto‘. All sorts of bad stuff went down during this time, much of which we’ve (thankfully) forgotten about. But TLS is the exception! Thanks to years of backwards compatibility requirements, it’s become a sort of time capsule for all sorts of embarrassing practices that should have died a long slow death in a moonlit graveyard.

For example:

  1. The vast majority of TLS handshakes use an RSA padding scheme known as PKCS#1v1.5. PKCS#1v1.5 is awesome — if you’re teaching a class on how to attack cryptographic protocols. In all other circumstances it sucks. The scheme was first broken all the way back in 1998. The attacks have gotten better since.
  2. The (AES)-CBC encryption used by SSL and TLS 1.0 is just plain broken, a fact that was recently exploited by the BEAST attack. TLS 1.1 and 1.2 fix the glaring bugs, but still use non-standard message authentication techniques, that have themselves been attacked.
  3. Today — in the year 2012 — the ‘recommended’ patch for the above issue is to switch to RC4. Really, the less said about this the better.

Although each of these issues have all been exploited in the past, I should be clear that current implementations do address them. Not by fixing the bugs, mind you — but rather, by applying band-aid patches to thwart the known attacks. This mostly works in practice, but it makes security proofs an exercise in frustration.

The second obstacle to proving things about TLS is the sheer complexity of the protocol. In fact, TLS is less a ‘protocol’ than it is a Frankenstein monster of of options and sub-protocols, all of which provide a breeding ground for bugs and attacks. Unfortunately, the vast majority of academic security analyses just ignore all of the ‘extra junk’ in favor of addressing the core crypto. Which is good! But also too bad — since these options where practically every real attack on TLS has taken place.

Lastly, it’s not clear quite which definition of security we should even use in our analysis. In part this is because the TLS specification doesn’t exactly scream ‘I want to be analyzed‘. In part it’s because definitions have been evolving over the years.

So you’re saying TLS is unprovable?

No. I’m just lowering expectations.

The truth is there’s a lot we do know about the security of TLS, some of it surprisingly positive. Several academic works have even given us formal ‘proofs’ of certain aspects of the protocol. The devil here lies mainly in the definitions of ‘proof‘ and — worryingly — ‘TLS‘.

For those who don’t live for the details, I’m going to start off by listing a few of the major known results here. In no particular order, these are:

  1. If properly implemented with a secure block cipher, the TLS 1.1/1.2 record encryption protocol meets a strong definition of (chosen ciphertext attack) security. Incidentally, the mechanism is also capable of hiding the length of the encrypted records. (Nobody even bothers to claim this for TLS 1.0 — which everybody agrees is busted.)
  2. A shiny new result from CRYPTO 2012 tells us that (a stripped-down version of) the Diffie-Hellman handshake (DHE) is provably secure in the ‘standard model’ of computation. Moreover, combined with result (1), the authors prove that TLS provides a secure channel for exchanging messages. Yay!This result is important — or would be, if more people actually used DHE. Unfortunately, at this point more people bike to work with their cat than use TLS-DHE.
  3. At least two excellent works have tackled the RSA-based handshake, which is the one most people actually use. Both works succeed in proving it secure, under one condition: you don’t actually use it! To be more explicit: both proofs quietly replace the PKCS#v1.5 padding (in actual use) with something better. If only the real world worked this way.
  4. All is not lost, however: back in 2003 Jonnson and Kaliski were able to prove security for the real RSA handshake without changing the protocol. Their proof is in the random oracle model (no biggie), but unfortunately it requires a new number-theoretic hardness assumption that nobody has talked about or revisited since. In practice this may be fine! Or it may not be. Nobody’s been able to investigate it further, since every researcher who tried to look into it… wound up dead. (No, I’m just kidding. Although that would be cool.) 
  5. A handful of works have attempted to analyze the entirety of SSL or TLS using machine-assisted proof techniques. This is incredibly ambitious, and moreover it’s probably the only real way to tackle the problem. Unfortunately, the proofs hugely simplify the underlying cryptography, and thus don’t cover the full range of attacks. Moreover, only computers can read them.

While I’m sure there are some important results I’m missing here, this is probably enough to take us 95% of the way to the ‘provable’ results on TLS. What remains is the details.

And oh boy, are there details. More than I can fit in one post. So I’m going to take this one chunk at a time, and see how many it takes.

An aside: what are we trying to prove, anyway?

One thing I’ve been a bit fast-and-loose on is: what are we actually proving about these protocols in the first place, anyway? The question deserves at least a few words — since it’s received thousands in the academic literature.

One obvious definition of security can be summed up as ‘an attacker on the wire can’t intercept modify data’, or otherwise learn the key being established. But simply keeping the data secret isn’t enough; there’s also a matter of freshness. Consider the following attack:

  1. I record communications between a legitimate client and his bank’s server, in which the client requests $5,000 to be transferred from her account to mine.
  2. Having done this, I replay the client’s messages to the server a hundred times. If all goes well, I’m  a whole lot richer.

Now this is just one example, but it shows that the protocol does require a bit of thinking. Taking this a step farther, we might also want to ensure that the master secret is random, meaning even if (one of) the Client or Server are dishonest, they can’t force the key to a chosen value. And beyond that, what we really care about is that the protocol data exchange is secure.

Various works take different approaches to defining security for TLS. This is not surprising, given the ‘security analysis‘ provided in the TLS spec itself is so incomplete that we don’t quite know what the protocol was intended to do in the first place. We’ll come back to these definitional issues in a bit.

The RSA handshake

TLS supports a number of different ciphersuites and handshake protocols. As I said above, the RSA-based handshake is the most popular one — almost an absurd margin. Sure, a few sites (notably Google) have recently begun supporting DHE and ECDH across the board. For everyone else there’s RSA.

So RSA seems as good a place as any to start. Even better, if you ignore client authentication and strip the handshake down to its core, it’s a pretty simple protocol:

Clearly the ‘engine’ of this protocol is the third step, where the Client picks a random 48-byte pre-master secret (PMS) and encrypts it under the server’s key. Since the Master Secret is derived from this (plus the Client and Server Randoms), an attacker who can’t ‘break’ this encryption shouldn’t be able to derive the Master Key and thus produce the correct check messages at the bottom.

So now for the $10,000,000 question: can we prove that the RSA encryption secure? And the simple answer is no, we can’t. This is because the encryption scheme used by TLS is RSA-PKCS#1v1.5, which is not — by itself — provably secure.

Indeed, it’s worse than that. Not only is PKCS#1v1.5 not provably secure, but it’s actually provably insecure. All the way back in 1998 Daniel Bleichenbacher demonstrated that PKCS#1v1.5 ciphertexts can be gradually decrypted, by repeatedly modifying them and sending the modified versions to be decrypted. If the decryptor (the server in this case) reveals whether the ciphertext is correctly formatted, the attacker can actually recover the encrypted PMS.

              0x 00 02 { at least 8 non-zero random bytes } 00 { two-byte length } { 48-byte PMS }

RSA-PKCS #1v1.5 encryption padding for TLS

Modern SSL/TLS servers are wise to this attack, and they deal with it in a simple way. Following decryption of the RSA ciphertext they check the padding. If it does not have the form above, they select a random PMS and go forward with the calculation of the Master Secret using this bogus replacement value. In principle, this means that the server calculates a basically random key — and the protocol doesn’t fail until the very end.

In practice this seems to work, but proving it is tricky! For one thing, it’s not enough to treat the RSA encryption as a black box — all of these extra steps and the subsequent calculation of the Master Secret are now intimately bound up with the security of the protocol, in a not-necessarily-straightforward way.

There are basically two ways to deal with this. Approach #1, taken by Morrisey, Smart and Warinschi and Gajek et al., follows what I call the ‘wishful thinking‘ paradigm. Both show that if you modify the encryption scheme used in TLS — for example, by eliminating the ‘random’ encryption padding, or swapping in a CCA-secure scheme like RSA-OAEP — the handshake is secure under a reasonable definition. This is very interesting from an academic point of view; it just doesn’t tell us much about TLS.

Fortunately there’s also the ‘realist‘ approach. This is embodied by an older CRYPTO paper by Jonnson and Kaliski. These authors considered the entirety of the TLS handshake, and showed that (1) if you model the PRF (or part of it) as a random oracle, and (2) assume some very non-standard number-theoretic assumptions, and (more importantly) (3) the TLS implementation is perfect, then you can actually prove that the RSA handshake is secure.

This is a big deal!

Unfortunately it has a few problems. First, it’s highly inelegant, and basically depends on all the parts working in tandem. If any part fails to work properly — if for example, the server leaks any information that could indicate whether the encryption padding is valid or not — then the entire thing crashes down. That the combined protocol works is in fact, more an accident of fate than the result of any real security engineering.

Secondly, the reduction extremely ‘loose’. This means that a literal interpretation would imply that we should be using ginormous RSA keys, much bigger than we do today. We obviously don’t pay attention to this result, and we’re probably right not to. Finally, it requires that we adopt odd number-theoretic assumption involving a ‘partial-RSA decision oracle’, something that quite frankly, feels kind of funny. While we’re all guilty of making up an assumption from time to time, I’ve never seen this assumption either before or since, and it’s significant that the scheme has no straightforward reduction the RSA problem (even in the random oracle model), something we would get if we used RSA-OAEP.

If your response is: who cares — well, you may be right. But this is where we stand.

So where are we?

Good question. We’ve learned quite a lot actually. When I started this post my assumption was that TLS was going to be a giant unprovable mess. Now that I’m halfway through this summary, my conclusion is that TLS is, well, still mostly a giant mess — but one that smacks of potential.

Of course so far I’ve only covered a small amount of ground. We still have yet to cover the big results, which deal with the Diffie-Hellman protocol, the actual encryption of data (yes, important!) and all the other crud that’s in the real protocol.

But those results will have to wait until the next post: I’ve hit my limit for today.

Click here for Part 2.

TACK

Those who read this blog know that I have a particular fascination with our CA system and how screwed up it is. The good news is that I’m not the only person who feels this way, and even better, there are a few people out there doing more than just talking about it.

Two of the ‘doers’ are Moxie Marlinspike and Trevor Perrin, who recently dropped TACK, a new proposal for ‘pinning’ TLS public keys. I would have written about TACK last week when it was fresh, but I was experimenting with a new approach to international travel where one doesn’t adjust oneself to the local timezone (nb: if you saw me and I was acting funny last week… sorry.)

TACK stands for Trust Assertions for Certificate Keys, but really, does it matter? TACK is one of those acronyms that’s much more descriptive in short form than long: it’s a way to ‘pin’ TLS servers to the correct public key even when a Certificate Authority is telling you differently, e.g., because the CA is misbehaving or has had its keys stolen.

In the rest of this post I’m going to give a quick overview of the problem that TACK tries to solve, and what TACK brings to the party.

Why do I need TACK?

For a long answer to this question you can see this previous post. But here’s the short version:

Because ‘secure communication’ on the Internet requires us to trust way too many people, many of of whom haven’t earned our trust, and probably couldn’t earn it if they tried.

Slightly less brief: most secure communication on the Internet is handled using the TLS protocol. TLS lets us communicate securely with anyone, even someone we’ve never met before.

While TLS is wonderful, it does have one limitation: it requires you to know the public key of the server you want to talk to. If an attacker can convince you to use the wrong public key (say, his key), you’ll end up talking securely to him instead. This is called a Man-in-the-Middle (MITM) attack and yes, it happens.

In principle we solve this problem using PKI. Any one of several hundred ‘trusted’ Certificate Authorities can digitally sign the server’s public key together with a domain name. The server sends the resulting certificate at the start of the protocol. If we trust all the CAs, life is good. But if any single one of those CAs lets us down, things get complicated.

And this is where the current CA model breaks down. Since every CA has the authority to sign any domain, a random CA in Malaysia can sign your US .com, even if you haven’t authorized it to, and even if that CA has never signed a .com before. It’s an invitation to abuse, since an attacker only need steal one CA private key anywhere in the world, and he can MITM any website.

The worst part of the ‘standard’ certificate model is how dumb it is. You’ve been connecting to your bank for a year, and each time it presented a particular public key certified by Verisign. Then one day that same site shows up with a brand new public key, signed by a CA from Guatemala. Should this raise flags? Probably. Will your browser warn you? Probably not. And this is where TACK comes in.

So what is TACK and how does it differ from other pinning schemes?

TACK is an extension to TLS that allows servers to ‘pin’ their public keys, essentially making the following statement to your TLS client:

This is a valid public key for this server. If you see anything else in this space, and I haven’t explicitly told you I’m changing keys, there’s something wrong.

Now, public-key pinning is not a new idea. A similar technique has been used by protocols like SSH for years, Google Chrome has a few static pins built in, and Google even has a draft HTTP extension that adds dynamic pinning capabilities to that protocol.

The problem with earlier pinning schemes is that they’re relatively inflexible. Big sites like Google and Facebook don’t run just one server, nor do they deploy a single public key. They run dozens or hundreds of servers, TLS terminators, etc., all configured with a mess of different keys and certificates. Moreover, configurations change frequently for business reasons. Pinning a particular public key to ‘facebook.com’ seems like a great idea, but probably isn’t as simple as you’d think it is. Moreover, a mistaken ‘pin’ is an invitation to a network disaster of epic proportions.

TACK takes an end-run around these problems, or rather, a couple of them:

  1. It adds a layer of indirection. Instead of pinning a particular TLS public key (either the server’s key, or some higher-level certificate public key), TACK pins sites to a totally separate ‘TACK key’ that’s not part of the certificates at all. You then use this key to make assertions about any of the keys on your system, even if each server uses a different one.
  2. It’s only temporary. A site pin lasts only a few days, no more than a month — unless you visit the site again to renew it. This puts pretty strict limits on the amount of damage you can do, e.g., by misconfiguring your pins, or by losing the TACK key.

So what exactly happens when I visit a TACK site?

So you’ve securely connected via TLS to https://facebook.com, which sports a valid certificate chain. Your browser also supports TACK. In addition to all the usual TLS negotiation junk, the server sends down a TACK public key in a new TLS extension field. It uses the corresponding TACK signing key to sign the server’s TLS public key. Next:

  1. Your browser makes note of the TACK key, but does nothing at all.
You see, it takes two separate connections to a website before any of the TACK machinery gets started. This is designed to insulate clients against the possibility that one connection might be an MITM.

The next time you connect, the server sends the same TACK public key/signature pair again, which activates the ‘pin’ — creating an association between ‘facebook.com’ and the TACK key, and telling your browser that this server public key is legitimate. If you last connected five days ago, then the ‘pin’ will be valid for five more days.

From here on out — until the TACK pin expires — your client will require that every TLS public key associated with facebook.com be signed by the TACK key. It doesn’t matter if Facebook has eight thousand different public keys, as long as each of those public keys gets shipped to the client along with a corresponding TACK signature. But if at any point your browser does not see a necessary signature, it will reject the connection as a possible MITM.

And that’s basically it.
The beauty of this approach is that the TACK key is entirely separate from the certificate keys. You can sign dozens of different server public keys with a single TACK key, and you can install new TLS certificates whenever you want. Clients’ browsers don’t care about this — the only data they need to store is that one TACK key and the association with facebook.com.

But what if I lose my TACK key or it gets stolen?

The nice thing about TACK is that it augments the existing CA infrastructure. Without a valid certificate chain (and a legitimate TLS connection), a TACK key is useless. Even if you lose the thing, it’s not a disaster, since pins expire relatively quickly. (Earlier proposals devote a lot of time to solving these problems, and even require you to back up your pinning keys.)

The best part is that the TACK signing key can remain offline. Unlike TLS private keys, the only thing the TACK key is used for is creating static signatures, which get stored on the various servers. This dramatically reduces the probability that the key will be stolen.

So is TACK the solution to everything?

TACK addresses a real problem with our existing TLS infrastructure, by allowing sites to (cleanly) set pins between server public keys and domain names. If widely deployed, this should help to protect us against the very real threat of MITM. It’s also potentially a great solution for those edge cases like MTA-to-MTA mailserver connections, where the PKI model actually doesn’t work very well, and pinning may be the most viable route to security.

But of course, TACK isn’t the answer to everything. The pins it sets are only temporary, and so a dedicated attacker with long-term access to a connection could probably manage to set incorrect pins. At the end of the day this seems pretty unlikely, but it’s certainly something to keep in mind.

If wishes were horses then beggars would ride… a Pwnie!

In case you’re wondering about the title above, I ripped it off from an old Belle Waring post on the subject of wishful thinking in politics. Her point (inspired by this Calvin & Hobbes strip) is that whenever you find yourself imagining how things should be in your preferred view of the world, there’s no reason to limit yourself. Just go for broke!

Take a non-political example. You want Facebook to offer free services, protect your privacy and shield you from targeted advertising? No problem! And while you’re wishing for those things, why not wish for a pony too!

This principle can also apply to engineering. As proof of this, I offer up a long conversation I just had with Dan Kaminsky on Twitter, related to the superiority of DNSSEC vs. application-layer solutions to securing email in transit. Short summary: Dan thinks DNSSEC will solve this problem, all we have to do is get it deployed everywhere in a reasonable amount of time. I agree with Dan. And while we’re daydreaming, ponies! (See how it works?)

The impetus for this discussion was a blog post by Tom Ritter, who points out that mail servers are horrendously insecure when it comes to shipping mail around the Internet. If you know your mailservers, there are basically two kinds of SMTP connection. MUA-to-MTA connections, where your mail client (say, Apple Mail) sends messages to an SMTP server such as GMail. And MTA-to-MTA connections, where Gmail sends the message on to a destination server (e.g., Hotmail).

Now, we’ve gotten pretty good at securing the client-to-server connections. In practice, this is usually done with TLS, using some standard server certificate that you can pick up from a reputable company like Trustwave. This works fine, since you know the location of your outgoing mail server and can request that the connection always use TLS.

Unfortunately, we truly suck at handling the next leg of the communication, where the email is shipped on to the next MTA, e.g., from Google to Hotmail. In many cases this connection isn’t encrypted at all, making it vulnerable to large-scale snooping. But even when it is secured, it’s not secured very well.

What Tom points out is that many mail servers (e.g., Gmail’s) don’t actually bother to use a valid TLS certificate on their MTA servers. Since this is the case, most email senders are configured to accept the bogus certs anyway, because everyone has basically given up on the system.

We could probably fix the certs, but you see, it doesn’t matter! That’s because finding that next MTA depends on a DNS lookup, and (standard) DNS is fundamentally insecure. A truly nasty MITM attacker can spoof the MX record returned, causing your server to believe that mail.evilempire.com is the appropriate server to receive Hotmail messages. And of course, mail.evilempire.com could have a perfectly legitimate certificate for its domain — which means you’d be hosed even if you checked it.

(It’s worth pointing out that the current X.509 certificate infrastructure does not have a universally-accepted field equivalent to “I am an authorized mailserver for Gmail”. It only covers hostnames.)

The question is, then, what to do about this?

There are at least three options. One is that we just suck it up and assume that email’s insecure anyway. If people want more security, they should end-to-end encrypt their mail with something like GPG. I’m totally sympathetic to this view, but I also recognize that almost nobody encrypts their email with GPG. Since we already support TLS on the MTA-to-MTA connection, perhaps we should be doing it securely?

The second view is that we fix this using some chimera of X.509 extensions and public-key pinning. In this proposal (inspired by an email from Adam Langley***), we’d slightly extend X.509 implementations to recognize an “I am a mailserver for Hotmail.com” field, we get CAs to sign these, and we install them on Hotmail’s servers. Of course, we’ll have to patch mailservers like Sendmail to actually check for these certs, and we’d have to be backwards compatible to servers that don’t support TLS at all — meaning we’d need to pin public keys to prevent downgrade attacks. It’s not a very elegant solution at all.

The third, ‘elegant’ view is that we handle all of our problems using DNSSEC. After all, this is what DNSSEC was built for! To send an email to Hotmail, my server just queries DNS for Hotmail.com, and (through the magic of public-key cryptography) it gets back a signed response guaranteeing that the MX record is legitimate. And a pony too!

But of course, back in the real world this is not at all what will happen, for one very simple reason:

  • Many mail services do not support DNSSEC for their mail servers.
  • Many operating systems do not support DNSSEC resolution. (e.g., Windows 8)

Ok, that’s two reasons, and I could probably add a few more. But at the end of the day DNSSEC is the pony with the long golden mane, the one your daughter wants you to buy her — right after you buy her the turtle and the fish and the little dog named Sparkles.

So maybe you think that I’m being totally unfair. If people truly want MTA-to-MTA connections to be secure, they’ll deploy DNSSEC and proper certificates. We’ll all modify Sendmail/Qmail/Etc. to validate that the DNS resolution is ‘secured’ and they’ll proceed appropriately. If DNS does not resolve securely, they’ll… they’ll…

Well, what will they do? It seems like there are only two answers to that question. Number one: when DNSSEC resolution fails (perhaps because it’s not supported by Hotmail), then the sender fails open. It accepts whatever insecure DNS response it can get, and we stick with the current broken approach. At least your email gets there.

Alternatively, we modify Sendmail to fail closed. When it fails to accomplish a secure DNS resolution, the email does not go out. This is the security-nerd approach.

Let me tell you something: Nobody likes the security-nerd approach.

As long as DNSSEC remains at pitiful levels of deployment, it’s not going to do much at all. Email providers probably won’t add DNSSEC support for MX records, since very few mailservers will be expecting it. Mailserver applications won’t employ (default, mandatory) DNSSEC checking because none of the providers will offer it! Around and around we’ll go.

But this isn’t just a case against DNSSEC, it relates to a larger security architecture question. Namely: when you’re designing a security system, beware of relying on things that are outside of your application boundary.

What I mean by this is that your application (or transport layer implementation, etc.) should not be dependent. If possible, it should try to achieve its security goals all by itself, with as few assumptions about the system that it’s running on, unless those assumptions are rock solid. If there’s any doubt that these assumptions will hold in practice, your system needs a credible fallback plan other than “ah, screw it” or “let’s be insecure”.

The dependence on a secure DNS infrastructure is one example of this boundary-breaking problem, but it’s not the only one.

For example, imagine that you’re writing an application depends on having a strong source of pseudo-random numbers. Of course you could get these from /dev/rand (or /dev/urand), but what if someone runs your application on a system that either (a) doesn’t have these, or (b) has them, but they’re terrible?

Now sometimes you make the choice to absorb a dependency, and you just move on. Maybe DNSSEC is a reasonable thing to rely on. But before you make that decision, you should also remember that it’s not just a question of your assumptions breaking down. There are human elements to think of.

Remember that you may understand your design, but if you’re going to be successful at all, someday you’ll have to turn it over to someone else. Possibly many someones. And those people need to understand the fullness of your design, meaning that if you made eight different assumptions, some of which occur outside of your control, then your new colleagues won’t just have eight different ways to screw things up. They’ll have 2^8 or n^8 different ways to screw it up.

You as the developer have a duty to yourself and to those future colleagues to keep your assumptions right there where you can keep an eye on them, unless you’re absolutely positively certain that you can rely on them holding in the future.

Anyway, that’s enough on this subject. There’s probably room on this blog for a longer and more detailed post about how DNSSEC works, and I’d like to write that post at some point. Dan obviously knows a lot more of the nitty-gritty than I do, and I’m (sort of) sympathetic to his position that DNSSEC is awesome. But that’s a post for the future. Not the DNSSEC-distant future, hopefully!

Notes:

* Dan informs me that he already has a Pwnie, hence the title.
** Thomas Ptacek also has a much more convincing (old) case against DNSSEC.
*** In fairness to Adam, I think his point was something like ‘this proposal is batsh*t insane’, maybe we should just stick with option (1). I may be wrong.

A tale of two patches

Nick Mathewson over at the Tor project points me to the latest vulnerability in OpenSSL’s implementation of TLS and DTLS (though only in some OpenSSL versions, YMMV). For those of you keeping score at home, this makes two serious flaws in the same small chunk of DTLS code in about four months.

I should note that Tor doesn’t use DTLS. In fact, based on a quick Google search, there may be more people with radioactive-spider-based superpowers than there are projects actually using OpenSSL DTLS (these folks being one possible exception). Moreover, it’s not clear that this bug (unlike the previous one) is useful for anything more than simple DoS.

But that doesn’t make it useless. Even if these things aren’t exploitable, bugs like this one provide us with the opportunity to learn something about how even ‘simple’ decryption code can go wrong. And that’s what we’re going to do in this post.

So let’s go take a look at the unpatched code in question.

This code handles the decryption of DTLS packets, and comes in a slightly older OpenSSL version, v1.0.0e (release 9/2011). To give you a flavor of how one could miss the first (less serious) issue, I was going to reproduce the entire 161-line megafunction in which the bug occurs. But it’s just too huge and awkward. Here’s the relevant bit:

int dtls1_enc(SSL *s, int send)
{
SSL3_RECORD *rec;
EVP_CIPHER_CTX *ds;
unsigned long l;
int bs,i,ii,j,k,n=0;
const EVP_CIPHER *enc; 
…
…        
if ((bs != 1) && !send)
  {
ii=i=rec->data[l-1]; /* padding_length */
i++;
if (s->options&SSL_OP_TLS_BLOCK_PADDING_BUG)
   {
/* First packet is even in size, so check */
if ((memcmp(s->s3->read_sequence,
                            “\0\0\0\0\0\0\0\0”,8) == 0) && !(ii & 1))
s->s3->flags|=TLS1_FLAGS_TLS_PADDING_BUG;
if (s->s3->flags & TLS1_FLAGS_TLS_PADDING_BUG)
i–;
   }
/* TLS 1.0 does not bound the number of padding bytes by the block size.
* All of them must have value ‘padding_length’. */
if (i > (int)rec->length)
   {
/* Incorrect padding. SSLerr() and ssl3_alert are done
* by caller: we don’t want to reveal whether this is
* a decryption error or a MAC verification failure
* (see http://www.openssl.org/~bodo/tls-cbc.txt) 
*/
return -1;
   }
for (j=(int)(l-i); j<(int)l; j++)
   {
if (rec->data[j] != ii)
      {
/* Incorrect padding */
return -1;
      }
   }
rec->length-=i;
            
rec->data += bs;    /* skip the implicit IV */
rec->input += bs;
rec->length -= bs;
   }
 }
return(1);
}

Now I could waste this whole post ranting about code quality, pointing out that variable names like ‘l’ and ‘bs’ were cute when Kernighan and his buddies were trying to get AWK small enough so they could write it down and type it in every day (or whatever they did for storage back then), but not so cute in 2012 inside of the most widely-used crypto library on earth.

I could also ask why this function is named “dtls1_enc” when in fact it actually contains decryption code as well as encryption code. I might even suggest that combining both operations into one massive, confusing function might have sounded like a better idea than it actually is.

But I’m not going to do all that, since that would be dull and the point of this post is to find a bug. So, do you see it? Hint: it’s in the boldfaced part.

Maybe I should give you a little more. Every DTLS packet begins with an ‘implicit’ Initialization Vector of length ‘bs’. The packet also comes with a bit of padding at the end, to bring the packet up to an even multiple of the cipher’s block size. Let ‘Mx’ represent message bytes and let ‘LL’ be the number of padding bytes expressed as a byte. Then the tail of the packet will look something like:

0x M1 M2 M3 M4 LL LL LL LL LL LL LL LL LL LL LL LL

An important note is that TLS 1.0 allows up to 255 padding bytes even if the blocksize is much less than that. So the last twenty-something lines of the boldfaced decryption code are basically checking the last byte of the decrypted message, then working backward through (possibly) multiple blocks of ‘bs’ bytes each, in order to strip off all of that ugly padding.

Do you see it now?

Ok, I’ll spoil it for you. The entirety of the bug comes in the statement “if (i > (int)rec->length)”, which ensures that the message is as long as the padding claims to be. What this doesn’t do is check that the Initialization Vector is there as well (update: I’ve edited this post a bit, since I got confused the first time!). Because of the missing check it’s possible to submit a short message that consists of only padding, in which case rec->length will be less than ‘bs’. At which point we flow through and hit this statement:

rec->length -= bs;

Oops. See what happens there? It might be helpful if I told you that rec->length is an unsigned long. So predictable consequences.

The OpenSSL folks describe this as a DoS vulnerability, not an exploitable one. I’m perfectly happy to take them at their word. But, yuck. This sort of stuff happens, I realize, but should it have to?

Since you’re still reading this, you’re obviously some kind of glutton for punishment. That probably means you’re going to stick around for the second (and somewhat older) issue, which was patched back in January. In fact, I wrote about it on this blog. To get there, you have to climb one level up to the caller of the function we just looked at.

This is easier said than done since — this being OpenSSL — of course the previous function isn’t called directly, it’s accessed via a function pointer! Oh lord. Ah, here we are:

static int
dtls1_process_record(SSL *s)
{
…
…
/* decrypt in place in ‘rr->input’ */
rr->data=rr->input;


enc_err = s->method->ssl3_enc->enc(s,0);  <<<<****** Call to the previous function!
if (enc_err <= 0)
 {
/* decryption failed, silently discard message */
if (enc_err < 0)
  {
rr->length = 0;
s->packet_length = 0;
  }
goto err;  <<<<****** Send an error message
}
…
…

/* check the MAC for rr->input (it’s in mac_size bytes at the tail) */
if (rr->length < mac_size)
  {
#if 0 /* OK only for stream ciphers */
al=SSL_AD_DECODE_ERROR;
SSLerr(SSL_F_DTLS1_PROCESS_RECORD,SSL_R_LENGTH_TOO_SHORT);
goto f_err;
#else
goto err;
#endif
  }
rr->length-=mac_size;
i=s->method->ssl3_enc->mac(s,md,0);
if (i data[rr->length]),mac_size) != 0)
  {
goto err;  <<<<****** Send an error message
  }
}
…
…
}
See it? Oh, maybe it will help if we revisit one of the bigger comments in the first function, the one that gets called:
 

/* Incorrect padding. SSLerr() and ssl3_alert are done
* by caller: we don’t want to reveal whether this is
* a decryption error or a MAC verification failure
* (see http://www.openssl.org/~bodo/tls-cbc.txt) 
*/
return -1;

Does that help? The people who wrote the first function knew full well how dangerous it is to reveal whether you’re failing due to a padding verification error or a MAC verification error. They even provided a link to the reason why!

Unfortunately the people writing the one-level up code didn’t understand the full implications of this, or didn’t realize that the information could leak out even if you don’t reveal exactly why you’ve barfed. People can learn why you failed even if there’s just a timing difference in when you give them the error code! This was known and mitigated in the TLS code, but not in the DTLS version.

And the end result is that there are two error conditions, occurring a significant distance from one another in the code. An attacker can monitor the decryption of chosen packets and use this information to slowly decrypt any plaintext. Ouch.

So what does it all mean?

You wanted meaning? I just wanted to look at some code.

But if I was to assign some arbitrary meaning to these mistakes, it’s that cryptographic code is frigging hard to write. And that more eyes does not necessarily mean fewer bugs, particularly if the code is messy and you have two versions doing substantially similar things (DTLS and TLS). It doesn’t help if your coding standard was basically invented on a dare.

OpenSSL has gotten to where it is today not for being a great library, but for basically being the library. And it’s certainly a good one, now that it’s been subjected to several years of unrelenting scrutiny. But the DTLS code is new and hasn’t received that same level of attention, which is why it’s fun to watch the bugs get shaken out all over again (unfortunately the first bug also appears in TLS code, which is harder to explain). I’m sure we haven’t seen the last of it.

An update on the TLS MITM situation

A couple months back I wrote a pretty overwrought post lamenting the broken state of our PKI. At the time, I was kind of upset that ‘trusted’ Certificate Authorities (*ahem*, Trustwave) had apparently made a business of selling that trust for the purpose of intercepting SSL/TLS connections.

Now, I may be off base, but this seems like a bad thing to me. It also seemed like pretty stupid business. After all, it’s not like certificates are hard to make (seriously — I made three while writing the previous sentence). When your sole distinguishing feature is that people trust you, why would you ever mess with that trust?

In any case, the worst part of the whole thing was a suspicion that the practice didn’t end with Trustwave; rather, that Trustwave was simply the CA that got caught. (No, this doesn’t make it better. Don’t even try that.)

But if that was the case, then who else was selling these man-in-the-middle ‘skeleton’ certificates? Who wasn’t? Could I just call up and order one today, or would it be all dark parking lots and windowless vans, like the last time I bought an 0day from VUPEN? (Kidding. Sort of.)

The saddest part of the whole story is that out of all the major browser vendors, only one — the Mozilla foundation, makers of Firefox — was willing to take public action on the issue. This came in the form of a letter that Mozilla sent to each of the major CAs in the Mozilla root program:

Please reply by March 2, 2012, to confirm completion of the following actions or state when these actions will be completed.

1) Subordinate CAs chaining to CAs in Mozilla’s root program cannot be used for MITM or “traffic management” of domain names or IPs that the certificate holder does not legitimately own or control, regardless of whether it is in a closed and controlled environment or not. Please review all of the subordinate CAs that chain up to your root certificates in NSS to make sure that they cannot be used in this way. Any existing subordinate CAs that can be used for that purpose must be revoked and any corresponding HSMs destroyed as soon as possible, but no later than April 27, 2012.

Which brings me to the point of this post. March 2 passed a long time ago. The results are mostly in. So what have we learned?


(Note: to read the linked spreadsheet, look at the column labeled “Action #1”. If it contains an A, B, or E, that means the CA has claimed innocence — it does not make SubCAs for signing MITM certificates, or else it does make SubCAs, but the holders are contractually-bound not to abuse them.* If there’s a C or a D there, it means that the CA is working the problem and will have things sorted out soon.)

The high-level overview is that most of the Certificate Authorities claim innocence. They simply don’t make SubCAs (now, anyway). If they do, they contractually require the holders not to use them for MITM eavesdropping. One hopes these contracts are enforceable. But on the surface, at least, things look ok.

There are a couple of exceptions: notably Verizon Business (in my hometown!), KEYNECTIS and GlobalSign. All three claim to have reasonable explanations, and are basically just requesting extensions so they can get their ducks in a row (KEYNECTIS is doing in-person inspections to make sure nothing funny is going on, which hopefully just means they’re super-diligent, and not that they’re picking up MITM boxes and throwing them in the trash.) **

But the upshot is that if we can believe this self-reported data, then Trustwave really was the outlier. They were the only people dumb enough to get into the business of selling SubCAs to their client for the purpose of intercepting TLS connections. Or at very least, the other players in this business knew it was a trap, and get themselves out long ago.

Anyone else believe this? I’d sure like to.

Notes:

* ‘Abuse’ here means signing certificates for domains that you don’t control. Yes, it’s unclear how strong these contracts are, and if there’s no possibility for abuse down the line. But we can only be so paranoid.

** I confess there some other aspects I don’t quite follow here — for example, why are some ‘compliant’ CAs marked with ‘CP/CPS does not allow MITM usage’, while others are ‘In Progress’ in making that change. I’m sure there’s a good technical reason for this. Hopefully the end result is compliance all around.

So long False Start, we hardly knew ye

Last week brought the sad news that Google is removing support for TLS False Start from the next version of Chrome. This follows on Google’s decision to withdraw TLS Snap Start, and caps off the long line of failures that started with the demise of Google Wave. Industry analysts are already debating the implications for Larry Page’s leadership and Google’s ‘Social’ strategy.

(I am, of course, being facetious.)

More seriously, it’s sad to see False Start go, since the engineering that led to False Start is one of the most innovative things happening in Internet security today. It’s also something that only Google can really do, since they make a browser and run a very popular service. The combination means they can try out new ideas on a broad scale without waiting for IETF approval and buy-in. Nor are they shy about doing this: when the Google team spots a problem, they tackle it head-on, in what I call the ‘nuke it from orbit’ approach. It’s kind of refreshing.

Of course, the flipside of experimentation is failure, and Google has seen its share of failed experiments. The last was Snap Start, which basically tackled the same problem as False Start, but in a different way. And now False Start is going the way of the coelacanth: it’ll still exist, but you’ll have a hard time finding it.

The response from the security community has been a lot of meaningful chin-tapping and moustache-stroking, but not (surprisingly) a lot of strong opinions. This is because — as we all recently discovered — none of us had really spent much time thinking about False Start before Google killed it.* And so now we’re all doing it retroactively.

What the heck is (was) False Start anyway?

Secure web (TLS) is dirt slow. At least, that’s the refrain you’ll hear from web companies that don’t deploy it. There are many objections but they usually boil down to two points: (1) TLS requires extra computing hardware on the server side, and (2) it adds latency to the user experience.

Why latency? Well, to answer that you only need to look at the TLS handshake. The handshake establishes a communication key between the server and client. It only needs to happen once per browsing session. Unfortunately it happens at the worst possible time: the first time you visit a new site. You never get a second chance to make a first impression.

Why is the standard handshake so slow? Short answer: key establishment requires two round trips — four ‘flights’ — before the client can send any actual data (say, an HTTP GET request). If you’re communicating via undersea cable, or if you’re using a mobile phone with a huge ping time (my AT&T phone just registered 250ms!) this is going to add up.

sy10660a
Standard TLS handshake (source). Application data exchange only occurs at step (9) in the diagram. Note that step (5) is optional, and steps (4),(7) can be conducted in the same message ‘flight’.

This is the problem that False Start tried to address. The designers — Langley, Modadugu and Moeller — approached this in the simplest possible way: they simply started sending data earlier.

You see, the bulk of the key exchange work in TLS really occurs in the first three messages, “client hello”, “server hello”, and “client key exchange”. By the time the client is ready to send this last message, it already knows the encryption key. Hence it can start transmitting encrypted data right then, cutting a full roundtrip off the handshake. The rest of the handshake is just ‘mop-up’: mostly dedicated to ensuring that nobody tampered with the handshake messages in-flight.

If your reaction to the previous sentence was: ‘isn’t it kind of important to know that nobody tampered with the handshake messages?‘, you’ve twigged to the primary security objection to False Start. But we’ll come back to that in a moment.

False Start sounds awesome: why did Google yank it?

The problem with False Start is that there are many servers (most, actually) that don’t support it. The good news is that many of them will tolerate FS. That is, if the Client starts sending data early, they’ll hold onto the data until they’ve finished their side of the handshake.

But not every server is so flexible. A small percentage of the servers on the Internet — mostly SSL terminators, according to Langley — really couldn’t handle False Start. They basically threw up all over it.

Google knew about this before deploying FS in Chrome, and had taken what I will loosely refer to as the ‘nuke it from orbit squared‘ approach. They scanned the Internet to compile a blacklist list of IPs that didn’t handle False Start, and they shipped it with Chrome. In principle this should have done the job.

Unfortunately, it didn’t. It seems that the non-FS-compatible servers were non-compliant in a weird non-deterministic way. A bunch looked good when Google scanned them, but really weren’t. These slipped past Google’s scan, and ultimately Google gave up on dealing with them. False Start was withdrawn.

Ok, it has issues. But is it secure?

From my point of view this is the much more interesting question. A bunch of smart folks (and also: me) wasted last Friday afternoon discussing this on Twitter. The general consensus is that we don’t really know.

The crux of the discussion is the Server “finished” message (#8 in the diagram above). This message is not in TLS just for show: it contains a hash over all of the handshake messages received by the server. This allows the client to verify that no ‘man in the middle’ is tampering with handshake messages, and in normal TLS it’s supposed to verify this before it sends any sensitive data.

This kind of tampering isn’t theoretical. In the bad old days of SSL2, it was possible to quietly downgrade the ciphersuite negotiation so that the Browser & Server would use an ‘export-weakened’ 40-bit cipher even when both wanted to use 128-bit keys. Integrity checks (mostly) eliminate this kind of threat.

The FS designers were wise to this threat, so they include some mitigations to deal with it. From the spec:

Clients and servers MUST NOT use the False Start protocol modification in a handshake unless the cipher suite uses a symmetric cipher that is considered cryptographically strong … While an attacker can change handshake messages to force a downgrade to a less secure symmetric cipher than otherwise would have been chosen, this rule ensures that in such a downgrade attack no application data will be sent under an insecure symmetric cipher.

While this seems to deal with the obvious threats (‘let’s not use encryption at all!’), it’s not clear that FS handles every possible MITM threat that could come up. For example, there were a number of mitigations proposed to deal with the BEAST attack — from basic things like ‘don’t use TLS 1.0’ to ‘activate the empty-fragment’ protection. There’s some reason to be fearful that these protections could be overwhelmed or disabled by an attacker who can tamper with handshake messages.

Note that this does not mean that False Start was actually vulnerable to any of the above. The last thing I want to do is claim a specific vulnerability in FS. Or rather, if I had a specific, concrete vulnerability, I’d be blogging about it.

Rather, the concern here is that TLS has taken a long time to get to the point it is now — and we’re still finding bugs (like BEAST). When you rip out parts of the anti-tamper machinery, you’re basically creating a whole new world of opportunities for clever (or even not-so-clever) attacks on the protocol. And that’s what I worry about.

Hands off my NSS

There’s one last brief point I’d like to mention about False Start and Snap Start, and that has to do with the implementation. If you’ve ever spent time with the NSS or OpenSSL code, you know that these are some of the finest examples of security coding in the world.

Haha, I kid. They’re terrifying.

Every time Google adds another extension (Snap Start, False Start, etc.), NSS gets patched. This additional patch code is small, and it’s written by great coders — but even so, this patching adds new cases and complexity to an already very messy library. It would be relatively easy for a bug to slip into one of these patches, or even the intersection of two patches. And this could affect more than just Google users.

In summary

It may seem a little odd to spend a whole blog post on a protocol that’s already been withdrawn, but really: it’s worth it. Examining protocols like False Start is the only way we learn; and making TLS faster is definitely something we want to learn about. Second, it’s not like False Start is the last we’ll hear from the Google TLS crew. It’ll certainly help if we’re up-to-speed when they release “False Start II: False Start with a Vengeance”.

Finally, False Start isn’t really dead — not yet, anyway. It lives on in Chrome for conducting Next Protocol Negotiation (NPN) transactions, used to negotiate SPDY.

On a final note, let me just say that I’m mostly enthusiastic about the work that Google is doing (modulo a few reservations noted above). I hope to see it continue, though I would like to see it get a little bit more outside scrutiny. After all, even though Google’s primarily acting as its own test case, many people use Chrome and Google! If they get something wrong, it won’t just be Google doing the suffering.

Notes:

* With some notable exceptions: see this great presentation by Nate Lawson.