Jacob Appelbaum tweets:

Does anyone have a good reading list on practically attacking RC4?

I don’t intend to give an exact answer to Jacob’s question here, but his tweet caught my eye for a reason. You see, just the other week I advised implementers to avoid RC4 — both because it’s easy to misuse, and because it’s has some real and theoretical flaws. But that doesn’t mean any particular RC4 implementation is broken.

Instead, you should take my advice as the crypto equivalent of “don’t run with scissors”, “don’t run near the pool”, or “don’t run near the pool while carrying scissors”. I don’t know anyone who’s actually lost an eye because they ignored these warnings, but I still yell this stuff at my kids. It’s common sense.

Still, this leaves us with a question: how bad is RC4, really?

RC4, the stream cipher for the rest of us

First, the basics. RC4 was invented in 1987 by Ron Rivest. It spent its first seven years as an RSA trade secret before it was eventually leaked to a public mailing list in 1994. The rest, as they say, is history.

You could argue that RC4’s rise was inevitable. By the time of its leak, it was already in widespread commercial use. Unlike DES it was fast in software.* More importantly, the scheme itself is dirt simple. You can fit the code for RC4 onto a cocktail napkin, with plenty of room left over for the cocktail. And of course, having become public, the ‘alleged’ RC4 was free.

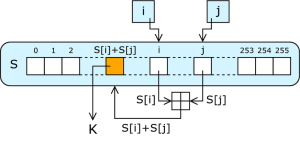
One phase of the RC4 PRG. K is the output byte. Image: Wikipedia.

The scheme consists of two parts: a key scheduling algorithm (KSA), and a pseudo-random generator (PRG). To encrypt a message, you run the key through the key scheduler, which produces a scrambled array called the state vector. You then feed the state vector into the PRG, which continuously permutes it while outputting a series of bytes. You then XOR those ‘keystream’ bytes with your plaintext.

RC4 is probably most famous for its (mis)use in 802.11 WEP. It’s still used in WPA-TKIP (unsurprising, since TKIP is just a bandaid patch for WEP). But its use goes way beyond that. For one thing, it’s a common ciphersuite for TLS, and as of a year or two ago it was even preferred by browsers like Chrome. Up until recently, Microsoft used it everywhere. Skype uses it to obfuscate (though not to encrypt) its communication protocol. It shows up in malware and a zillion crappy DRM packages.

To make a long story short, you’ll usually find RC4 anywhere the hardware was too weak, or the developers too lazy to use a better cipher.

The plain stupid

There are a few basic things you need to avoid when using any PRG-based cipher. These aren’t specific to RC4, but for some reason they seem to crop up at a higher rate in RC4 implementations than with other ciphers.

The big honking obvious one is that you can’t re-use the same RC4 keystream to encrypt two different messages. I hope I don’t need to go into the consequences, but they’re bad. Don’t do it.

You’d think this is so obvious that nobody could get it wrong, but that’s exactly what Microsoft famously did back in 2005, encrypting different versions of a Word document with the same key. If you must use the same key for different messages, the solution is to combine the key with an Initialization Vector or ‘nonce’. Unfortunately this can be problematic as well.

Another big issue is ciphertext malleability. If you flip a bit in an RC4 ciphertext, you’ll see the same bit flipped in the decrypted plaintext. This is awesome at parties. More to the point, it can lead to practical padding-oracle type attacks that totally compromise the security of your encryption.**

The solution to the latter problem is simply to MAC your ciphertexts. Unfortunately, people don’t use RC4 because they know what a MAC is — they use RC4 because you can download the code from Wikipedia. So, again, while this can happen with many ciphers, it tends to happen with RC4 a lot more than it should.

Key Scheduling

Leaving aside the stupid, the real problem with RC4 is the Key Scheduling Algorithm (KSA), which kind of sucks.

Picture a brand new box of playing cards. Starting with the unshuffled deck, work systematically from top to bottom, swapping each card’s position with another card in the deck. The position you’re swapping to is determined by a few simple computations involving the original card’s face value and the cryptographic key. Now do this with a stack of about five ordered decks and you’ve got the RC4 KSA.

While this shuffle seems thorough, the devil is in those simple computations. Ultimately their simplicity means the shuffle isn’t unpredictable enough. This leads to predictable patterns that show up in the first PRG output bytes. For example, Mantin and Shamir noted that the second output byte takes on the value ‘0’ with about twice the probability it should. By itself that may not seem terribly useful, but for one thing: it’s enough to practically determine whether an unknown algorithm is RC4, given about 128 keystreams on different (random) keys.

From what I can tell, the first person to notice problems with KSA was Andrew Roos, who posted a paper to sci.crypt about a year after the leak. Aside from the fact that it was published on Usenet, Roos’s result is notable for two reasons. First, he correctly identified use of concatenated IVs as a likely source of weakness in WEP implementations — years before anyone else did. Second, Roos gave recommendations that — had they been followed — could have prevented a lot of subsequent heartache. (Lesson: don’t publish scientific results in newsgroups.)

FMS

Roos’s paper set the table for the most famous attack on RC4, and the one that people still associate with RC4, even though it’s rarely used in its original form. This is, of course, the Fluhrer, Mantin and Shamir, or ‘FMS’ attack, which appeared in 2001.

Just like Roos, FMS looked at the KSA and found it wanting — specifically, they discovered that for certain weak keys, the first byte output by the PRG tends to be correlated to bytes of the key. These weak keys can be obtained by prepending a few chosen bytes (say, 3 of them) to an unknown, fixed, secret key. Given keystreams resulting from 60 such chosen keys, you can derive one byte of the secret portion of the key. A 16-byte key can therefore be computed from about 960 such keystreams.

On the face of it this sounds pretty unlikely — after all, how are you going to get an encryptor to prepend chosen bytes to their secret key. Fortunately the attack works fine even if the adversary just knows that the appropriate bytes were used. This works perfectly for implementations that prepend (or append) a known Initialization Vector to the WEP key. Simply by observing a few million IVs, an attacker can eventually collect enough keystreams to meet the FMS requirements.

All of this would have be a historical footnote if it hadn’t been for protocols like WEP, which (among its many problems) used a three-byte prepended IV. FMS was quickly demonstrated to work on WEP, then packaged into a neat tool and distributed.

Klein, Dropping and Hashing

There are two common approaches to dealing with the FMS attack:

1. Drop the first N bytes of the RC4 keystream, for values of N ranging from 256 to 3,072.
2. Don’t concatenate the IV to the key, hash the two together instead.

The first option is sometimes referred to as RC4-drop[N], and the actual value of N has been subject to some debate. In 2006, Klein presented a super-charged variant of the FMS attack that reduced the necessary number of IVs from millions down to about 25,000. More importantly, he showed that FMS-type attacks are still (borderline) viable even if you drop the first 256 bytes of the keystream. So 768 seems like a bare minimum to me, and some people will argue for much larger values.

The second approach was adopted for WPA-TKIP, which was proposed as a band-aid replacement for WEP. TKIP was designed to support legacy WEP-capable devices that had internal RC4 hardware, but weren’t powerful enough to handle AES. It made a bunch of positive changes to WEP (including adding a larger IV to prevent keystream reuse), but the most notable change was a new custom hash function that creates a per-packet key from an IV and secret key.

As a hash function, the TKIP hash kind of stinks. For one thing, it can be inverted given only about 10 per-packet keys and about 2^32 computation (these days, a few minutes on a TI calculator). However, this isn’t as big of a deal as it sounds: pre-image resistance isn’t precisely a goal of the TKIP hash, since those per-packet keys themselves should themselves be hard to obtain. Nonetheless, I wouldn’t recommend that you mess around with it. If you must use RC4, try a proper hash function. Or better yet, don’t use RC4 at all.

Distinguishers

So is RC4 a good pseudo-random generator? Meh. Given a mere 1.5GB of keystream data, Fluhrer and McGrew presented an algorithm that distinguishes RC4 from random. I already mentioned Mantin and Shamir who cranked this down to about 256 bytes (over various unknown, unrelated keys) by looking at the second output byte. Finally, Mantin noticed the presence of repeating patterns in RC4, which aren’t simply dependent on the first few bytes of output, and can be used to distinguish RC4 given about 64MB of keystream.

There are, of course, other distinguishing attacks. But does it matter?

Well, sort of. Indistinguishability is a critical characteristic of an XOR-based stream cipher. If we have it, then the security argument for RC4 encryption is very simple: to an adversary who can’t distinguish the PRG, RC4 encryption is indistinguishable from using a one-time pad.

Unfortunately the converse isn’t true. Just because RC4 output is distinguishable from random doesn’t mean that there’s a practical attack on the cipher. These results are important mostly because they illustrate the fundamental wonkiness of RC4, wonkiness that doesn’t go away just because you drop the first 3,072 bytes. But they don’t exactly give us a practical opening into the cipher itself. Yet.

Ok, none of this was very helpful. I just want to know: can I use RC4?

Great question.

The upshot is that RC4, if used as recommended (with hashed IVs and/or dropped output and MACs), is perfectly sufficient for securely encrypting messages. Today. The problem is, we never know what the future will bring.

My advice? Don’t run with scissors. You can lose an eye that way.

Notes:

* My totally unscientific results, from running ‘openssl speed’ on a lightly loaded Macbook Pro: 3DES-EDE: 21 bytes/μsec. DES: 54 bytes/μsec. AES-128: 118 bytes/μsec. RC4: 248 bytes/μsec.

** You might argue that RC4 implementations shouldn’t use padding in the first place, since (unlike CBC mode encryption with a block cipher) messages don’t need to be padded to a multiple of a block size. This is true — however, I would note that ‘padding oracle’-style attacks needn’t rely specifically on padding. Padding is just one type of encoding that can leak useful information if used incorrectly. For a great example, see Jager and Somorovsky’s recent result that uses UTF8 coding checks to defeat XML encryption.

*** By reasonable, of course, we mean ‘computationally limited’. This rules out attacks that require an unrealistically long time, quantum computing, or ESP.